Prove that $(a-d)^2+(b-c)^2\geq 1.6$ if $a^2+4b^2=4$ and $cd=4$

Question

Let $a, b, c, d$ be real numbers. I need to prove this innocent inequality $$ (a-d)^2+(b-c)^2\geq 1.6 $$ if $a^2+4b^2=4$ and $cd=4$.

I was told that there exist nice and sweet elementary solutions.

Answer 1

If I remember it right, I saw this inequality long ago, when I was a schoolboy. Then I didn’t solve it. But now it seems the following for me.

Of course, the geometric approach is the first solution idea, :-) but it should be developed. Without loss of generality, it suffices to consider Quadrant I of the plane (the disposition in the Quadrant III is symmetric).

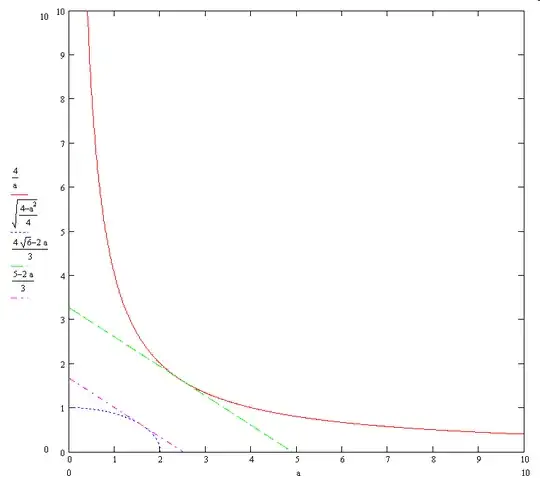
We try to find the parallel lines separating the curves. The experimental evidence suggests to try $2a+3b=x$ and $2d+3c=y$ (see the picture).

The first line. In the coordinates $(a/2,b)$ the line is a tangent to the unit circle. It these coordinates the line has the equation $4(a/2)+3b=x$. Therefore it is tangent to the circle at the point $(4,3)/\sqrt{4^2+3^2}=(4/5,3/5)$. Then $x=(4\cdot (4/5)+3\cdot (3/5))=5$.

The second line. $2d+3b\ge 2\sqrt{2d\cdot 3b}=4\sqrt 6=y$.

The squared distance between the lines is $\frac {(x-y)^2}{2^2+3^2}=1.77\dots>1.6$.

Answer 2

Using $a^2 + 4b^2 = 4$ and $cd = 4$, we have \begin{align*} &(a - d)^2 + (b - c)^2 + \frac12(a^2 + 4b^2 - 4) - \frac{2\sqrt 2}{3}(cd - 4)\\[6pt] =\,& \frac16(3a - 2d)^2 + \frac13(3b - c)^2 + \frac13(d - c\sqrt 2)^2 + \frac{8\sqrt 2}{3} - 2 \\[6pt] \ge\, &\frac{8\sqrt 2}{3} - 2\\ >\,& \frac85. \end{align*} We are done.

Answer 3

it is supplementary to Alex's method which more like high school method:

The idea is same,we use two parallel lines to calculate. let slop is $k=-\tan{ \alpha}, 0<\alpha <\dfrac{\pi}{2}$,

the tangent line to ellipse $x^2+4y^2=4$ is :$y=kx+b_1 \to x^2+4(kx+b_1)^2=4, \Delta=0,\implies b_1^2=4k^2+1$

the tangent line to Hyperbola $xy=4$ is:$y=kx+b \to x(kx+b)=4, \Delta=0,\implies k=-\dfrac{b^2}{4^2}$

$b_1=\sqrt{\dfrac{b^4}{64}+1},\cos{\alpha}=\dfrac{1}{\sqrt{1+\tan^2{\alpha}}}=\dfrac{4^2}{\sqrt{b^4+4^4}}$

the distance between two lines is: $D=(b-b_1)\cos{\alpha}=\left(b-\sqrt{\dfrac{b^4}{64}+1}\right)\dfrac{4^2}{\sqrt{b^4+4^4}}=\dfrac{2(8b-\sqrt{b^4+64})}{\sqrt{b^4+4^4}}=\dfrac{2(64b^2-b^4-64)}{\sqrt{b^4+4^4}(b+\sqrt{b^4+64})}=\dfrac{2(960-(b^2-32^2)^2)}{\sqrt{b^4+4^4}(b+\sqrt{b^4+64})}$

the numerator is Parabola, the peak is at $b^2=32,b=4\sqrt{2}$

the denominator is mono increasing function, and it is lead by $b^4$, so it will cause the peak of $D$ move left strongly. The $D(b)$ has two zero points at about $b=1,8$, so the peak point should be around $3$ or $4$( it is guess).

$D(3)=1.3,D(4)=1.25 \implies D^2=1.69>1.6$ so we have at least one solution to show the square of distance of two points $(a,b),(c,d) >1.6 $

if we try $D(3.5)=1.76$, so if we set min is $1.7$,it is much hard to high school student.

Answer 4

If $a^2+4b^2=4$ , we have an ellipse with width $2$ and height $1$. Now, the set of points $cd=4$ describes a hyperbola which does not cross the ellipse. You need to prove that: $$(a-d)^2 + (b-c)^2 \geq 1.6$$ This is equation for a circle centered around the point $(c,d)$ which lies on the hyperbola. In other words, your problem is to prove that the hyperbola is always at least $1.6$ units away from the ellipse.

Therefore, it is enough to find the minimal distance between the functions: $$f(x) = \frac{4}{x},\ \ g(x) = \sqrt{\frac{4 - x^2}{4}}$$ And to show that this is larger than $1.6$, i.e. find the minimum of:

$$\min_{x_1,x_2} \sqrt{\left( \frac{4}{x_1} - \sqrt{\frac{4 - x_2^2}{4}} \right)^2 -(x_1-x_2)^2}$$ In the range $x_2\in[0,2]$, $x_1>0$.