Find maximum of $xy$ subject to $(x+1)^2 + y^2 = 4$ without using Calculus techniques

Question

Find maximum of $xy$ subject to $(x+1)^2 + y^2 = 4$.

It is easy if we apply Calculus techniques (e.g., derivatives, Lagrange multipliers, etc). However, the problem is assigned for students who have not yet learned Calculus. Is there a way to find the maximum without using Calculus techniques?

I have a few ideas:

1. Apply geometric means: $xy \leq \frac{x^2+y^2}{2} = -x + 3/2 $.

2. Change object function to $(xy)^2$, then we have $(xy)^2 = x^2(4-(x+1)^2)=x^2(-x^2 - 2x +3)$. That is, maximize $x^2(-x^2 - 2x +3)$ on $(-3,1)$.

Answer 1

If you are deadset on a way without calculus, lets start with your idea $2$, i.e. how to maximize $$p(x) = x^2y^2 = x^2\left(4-(x+1)^2 \right)= x^2(1-x)(3+x)$$

Now it is evident that this is a downward facing quartic with roots (with multiplicity) $-3, 0, 0, 1$, so the function is positive when $x \in (-3, 0)$ or $(0, 1)$. It must have maxima in those intervals and one of them must be the global maximum we seek.

Case $1$: $x \in (-3, 0)$
$$p = (-x)(-x) (1-x)(3+x)$$ is a product of four positive terms, so by AM-GM, if the sum were a constant this would be maximized when all terms are equal. Unfortunately the sum is not a constant, and the equality condition $(-x) = (1-x)$ is absurd. Both these problems however can be addressed by appropriate scaling. So consider maximizing for some real $\alpha, \beta > 0$, $$\alpha \beta p = (-x)(-x)(\alpha - \alpha x)(3\beta + \beta x)$$ Now the sum is a constant if we have $2+\alpha = \beta$ and for equality we must have $-x = \alpha -\alpha x = 3\beta + \beta x \implies \alpha = \frac14(\sqrt{33}-3), \beta = \frac14(5+\sqrt{33}), x = -\frac14(3+\sqrt{33})$

As all the conditions for AM-GM get satisfied here, the maximum in $(-3,0)$ is when $x = -\frac14(3+\sqrt{33}) = x_1$, say.

Case $2$: $x \in (0, 1)$
Following the same logic, we now have $$\alpha \beta p = (x)(x)(\alpha-\alpha x)(3\beta+\beta x)$$ and the conditions give $2+\beta = \alpha, x = \alpha - \alpha x = 3\beta + \beta x \implies x_2 = \frac14(\sqrt{33}-3)$

All that is left is to see which among $x_1, x_2$ gives you the maximum, and it is easily seen $p(x_1) > p(x_2)$, so the maximum is $\sqrt{p(x_1)} = \frac14\sqrt{\frac32(69+11\sqrt{33})} \approx 3.52$.

Answer 2

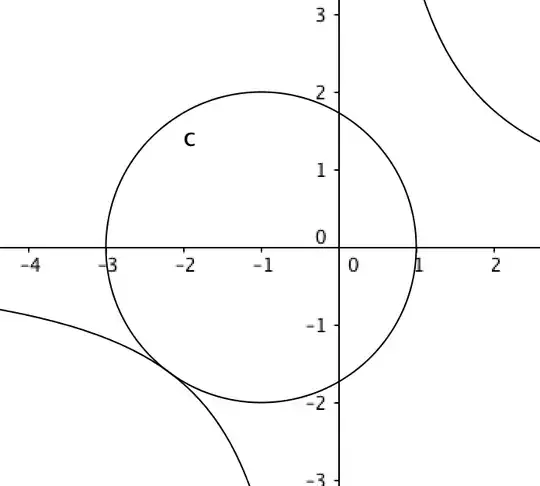
Your constraint is a circle centered at $(-1,0)$ with radius $2$. And the level curves of $xy$ with positive level are hyperbolae in the first and third quadrant. Since the circle is centered left of the origin, visualizing this it should be clear that the maximum value of $xy$ happens when both $x$ and $y$ are negative.

Furthermore, the curve $xy=M$ (where $M$ is the maximal value subject to the constraint) must intersect the circle in a tangency instead of at crossings, or else a slightly larger $M$ would be obtainable. For these two curves to intersect with tangency, there must be a repeated root to the equation that you get by eliminating one variable.

That is, if you eliminate $y$ to get $$(x+1)^2+\left(\frac{M}{x}\right)^2=4$$ and then expand and clear $x$ from the denominator to get $$x^4+2x^3-3x^2+M^2=0$$ we need to have a polynomial equation with a doubled root. So for some $a,b,c$:

$$\begin{align} &x^4+2x^3-3x^2+M^2\\ &=(x-a)^2(x-b)(x-c)\\ &=(x^2-2ax+a^2)(x^2-(b+c)x+bc)\\ &=x^4-(2a+b+c)x^3+(a^2+2a(b+c)+bc)x^2-(a^2(b+c)+2abc)x+a^2bc\\ \end{align}$$

which implies the system $$\begin{cases} 2a+b+c&=-2\\ a^2+2a(b+c)+bc&=-3\\ a^2b+a^2c+2abc&=0 \end{cases}$$

In the last equation we know $a\neq0$ so we can divide by $a$. Then we can eliminate $c$ by solving for it in the first equation and substituting it into the other two. All this gives: $$\begin{cases} -4a-3a^2-2b-2ab-b^2&=-3\\ -2a-2a^2-4b-4ab-2b^2&=0 \end{cases}$$

Double the top and subtract from the second to get: $$6a+4a^2=6$$ from which we can solve for $a$ using the quadratic formula. Remember that $a$ is the doubled root, and so it is the same as the $x$-value where $xy$ is maximal. Also we know this number is negative, which helps to discern between the two quadratic solutions. We find that $x=a=-\frac14\left(3+\sqrt{33}\right)$ at the point where $xy$ is maximal.

Now we can find: $$\begin{align} y&=-\sqrt{4-(x+1)^2}\\ &=-\sqrt{4-\left(-\frac14\left(3+\sqrt{33}\right)+1\right)^2}\\ &=-\sqrt{4-\left(\frac14\left(1-\sqrt{33}\right)\right)^2}\\ &=-\sqrt{4-\frac1{16}\left(34-2\sqrt{33}\right)}\\ &=-\frac14\sqrt{30+2\sqrt{33}} \end{align}$$

And so the maximal value is $$M=xy=\frac{1}{16}\left(3+\sqrt{33}\right)\sqrt{30+2\sqrt{33}}$$

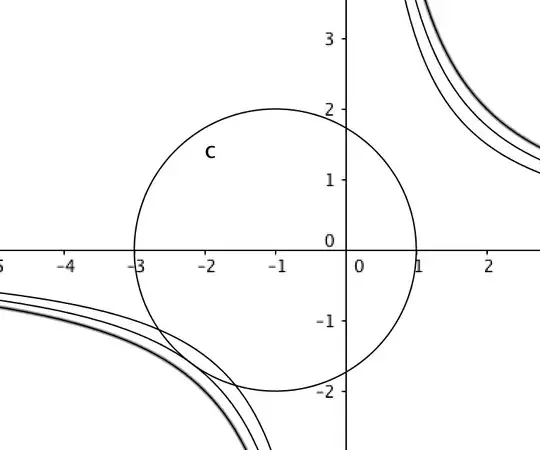
I submit visual evidence that this is the maximal value. A plot of the circle and the curve $xy=M$. A larger $M$, and the two curves would not intersect.

Answer 3

Here is perhaps a shorter way to solve it without calculus. At an extremum we have a turning point, or the tangent is horizontal - so we may translate the graph to get a polynomial multiple of $x^2$. Note that if $p(x) = x^2(4-(x+1)^2)$, then

$$p(x+a)+C = x^2Q(x) - 2a(2a^2+3a-3)x+(C - a^2(1-a)^2(3+a))$$

now if there is an extremum, for some $a, C$ the polynomial above must have no linear or constant term. The constant term can always be set to zero by appropriate choice of $C$, but we will also need the linear term to have zero coefficient. $a=0$ corresponds to the known double root / minimum at $x=0$, hence we need

$$2a^2+3a-3 = 0 \implies a = -\tfrac14(3 \pm \sqrt{33})$$

Now all that is left is to test which root gives the larger value.

Answer 4

Remarks: Note that the objective function and the constraint are both quadratic. Here I introduce a trick for this type of problems. I used this trick for these problems: P1, P2(see Discussion there), and (non-quadratic) P3.

The trick is to find real constants $M$ and $s$ (if any) such that $$f(x, y) := M - xy + s[(x + 1)^2 + y^2 - 4] \ge 0, \quad \forall x, y\in \mathbb{R}. \tag{1}$$

Clearly, $s \ne 0$. After completing the square in $y, x$ (one at a time), we have $$f(x, y) = s\left(y - \frac{x}{2s}\right)^2 + \frac{4s^2 - 1}{4s}\left(x + \frac{4s^2}{4s^2 - 1}\right)^2 + M - \frac{16s^3 - 3s}{4s^2 - 1}. \tag{2} $$ We have $s > 0$ and $\frac{4s^2 - 1}{4s} > 0$ which gives $s > 1/2$.

It can be seen from (2) that the minimum of $f(x, y)$ occurs when $$x = -\frac{4s^2}{4s^2 - 1}, \quad y = \frac{x}{2s} = - \frac{2s}{4s^2 - 1}. \tag{3}$$

Inserting (3) into the constraint $(x+1)^2 + y^2 = 4$, we have $$- \frac{64s^4 - 36s^2 + 3}{(4s^2 - 1)^2} = 0$$ which results in (using $s > 1/2$) $$s = \frac18\sqrt{18 + 2\sqrt{33}}.$$

If we choose $$M = \frac{16s^3 - 3s}{4s^2 - 1} = \frac{1}{32}\sqrt{18 + 2\sqrt{33}}\, (15 + \sqrt{33}) \approx 3.520345188,$$ then we have the following $$\frac{1}{32}\sqrt{18 + 2\sqrt{33}}\, (15 + \sqrt{33}) - xy + \frac18\sqrt{18 + 2\sqrt{33}}\,[(x + 1)^2 + y^2 - 4] \ge 0 \tag{4}$$ for all reals $x, y$.

It is easy to check that $\frac{1}{32}\sqrt{18 + 2\sqrt{33}}\, (15 + \sqrt{33})$ is indeed the maximum.

We are done.

Note: The result is the same as the other two answers. Indeed, $\frac14\sqrt{\frac32(69+11\sqrt{33})} = \frac{1}{16}\left(3+\sqrt{33}\right)\sqrt{30+2\sqrt{33}} = \frac{1}{32}\sqrt{18 + 2\sqrt{33}}\, (15 + \sqrt{33})$.

Answer 5

Maximizing $xy$ in this context is equivalent to maximizing $x^2y^2$. So let's do that instead, and subject to the constraint, we are maximizing $$x^2\left(4-(x+1)^2\right)=-x^4-2x^3+3x^2$$ Instead let's minimize the following, to avoid the leading negative sign: $$x^4+2x^3-3x^2$$ Changing variables with $x=\frac12(b-1)$ and then rescaling it all by $16$ gets us a depressed quartic: $$b^4-18b^2+32b-15$$ Keep in mind the general shape of a quartic's graph. There is a lowest point (possibly two local low points). Minimizing this means what number $(15+c)$ could we add to this from this to make it have a doubled root with the other roots nonreal? After adding $(15+c)$: $$b^4-18b^2+32b+c$$ Having a doubled root happens if and only if the (quartic) discriminant is zero. The formula for a quartic discriminant is honestly not something I have memorized, but if you are willing to look it up, we get $$16(-18)^4c-4(-18)^3(32)^2-128(-18)^2c^2+144(-18)(32)^2c-27(32)^4+256c^3=0$$ Expanding this and dividing out $256$: $$c^3-162c^2-3807c-17280=0$$ Our original expression back up in the first line already had a doubled root. So certainly $c=-15$ is a root of this cubic in $c$, and that means $(c+15)$ is a factor. Factor it out: $$(c+15)\left(c^2-177c-1152\right)=0$$ There are two other roots for $c$. We want the greatet one so that $(15+c)$ will be the greatest number that leaves $b^4-18b^2+32b+c$ with one real doubled root and no more real roots. (Visually, it brings the low point up to the $y$-axis.) $$c=\frac12\left(177+\sqrt{177^2-4(-1152)}\right)=\frac12\left(177+33\sqrt{33}\right)$$

Adding $(15+c)$ to $b^4-18b^2+32b-15$ is how we bring the minimum of $b^4-18b^2+32b-15$ up to zero. So the minimum value of $b^4-18b^2+32b-15$ is $$-(15+c)=-\frac12\left(207+33\sqrt{33}\right)$$

At one point we scaled by $16$. We also negated everything early on. So the maximum value of $x^2y^2$ should be $$\frac1{32}\left(207+33\sqrt{33}\right)$$

But then the maximum value for $xy$ is the square root of this: $$\frac18\sqrt{414+66\sqrt{33}}$$

Answer 6

To avoid using the Lagrange multipliers you may use the geometric property of extremals. At the extremal point, the gradient of the circle $\bf c$, and the gradient of the hyperbola, $\bf h$, are parallel. Thus solve a system of two equations for $x $ and $y $:

1. Equation of the circle
2. $\frac {c_x}{h_x} = \frac {c_y}{h_y}$ (or its reciprocal).