9

I have some questions regarding the Invariance Principle commonly used in contest math. It is well known that even though invariants can make problems easier to solve, finding invariants can be really, really hard. There is this problem from Arthur Engel's book titled "Problem Solving Strategies" which states:

In a regular hexagon all diagonals are drawn. Initially each vertex and each point of intersection of the diagonals is labeled by the number 1. In one step it is permitted to change the signs of all numbers of a side or diagonal. Is it possible to change the signs of all labels to −1 by a sequence of steps?

We are supposed to use invariance in this problem. I am very bad at locating the invariant unless it is something as simple as modn of some value in the problem for a particular value of n. I could not solve this problem using an invariant; however, I solved it by arguing that if the center point S of the attached figure carries number -1 along with the points 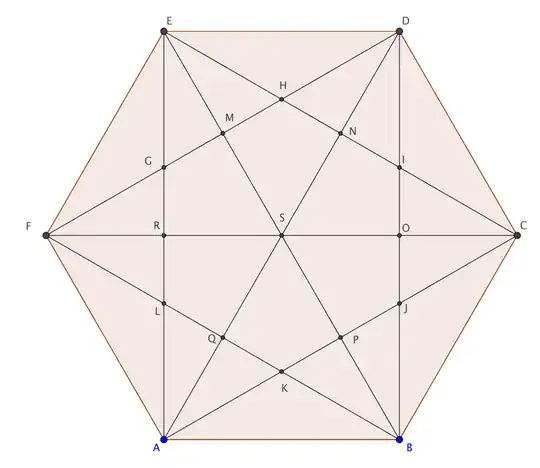enter image description here N, H, Q and L, then G will be forced to be +1. I am not elaborating on the complete solution, as that is a distraction from my main question.

Engel's solution feels like she or he is a genius who came up with it. Referring to the figure again, we can see that the product of the nine numbers on M, H, N, O, J, P, Q, L, and R does not change (another figure shown below to picture it better).

enter image description here

Everytime I managed to solve an invariance-based problem, I solved it by not using Invariance Principle. I have two questions.

  1. How do you get better at applying the Invariance Principle? I have solved a lot of problems and managed to solve ... maybe only 60% of what I attempted. I want to reach at least 80 to 90% of success rate.

  2. Are there other good sources for invariance-based problems? I am almost done with Arthur Engel's "Problem Solving Strategies" and I am completely done with Paul Zeitz's "The Art and Craft of Problem Solving" as far as invariance chapter is concerned.

Invariance has been one of my biggest handicaps in problem solving. I would greatly appreciate it if you can please answer the two questions above.

Community
  • 1
TryingHardToBecomeAGoodPrSlvr
  • 1,512
  • My biggest handicaps so far so is Invariance and Functional Equations.I need help and I mean it. – Icosahedron Aug 08 '17 at 21:19
  • 1
    @Icosahedron I am also in the same boat. For functional equations, there are books dealing with it. There are also some nice handouts available. But invariance is a beast and I have not found any good books on that topic. I wish someone on this forum would recommend a good source of problems (at the level of IMO/Putnam) for Invariance. – TryingHardToBecomeAGoodPrSlvr Aug 08 '17 at 22:35
  • I wish you luck buddy, I have Engel too here, I understand the simple problems but when asked to solve a difficult problem, I end up solving it without invariance just like you said. I'll mention you in a thread whenever I see a good textbook devoted to this topic, also, can you share me some useful resources on Functional equations? – Icosahedron Aug 08 '17 at 22:55
  • There are a lot of books and resources for functional equations. I will mention a few here. Evan Chen's handout -- link: http://web.evanchen.cc/handouts/FuncEq-Intro/FuncEq-Intro.pdf, B. J. Venkatachala's book -- B. J. Venkatachala. Functional Equations: A Problem Solving Approach -- Amazon link: http://www.amazon.in/Functional-Equations-Problem-Solving-Approach/dp/8172862652, Titu Andreescu's book titled Topics in Functional Equations -- Amazon link: https://www.amazon.com/Topics-Functional-Equations-Titu-Andreescu/dp/0979926998. Hope this helps. – TryingHardToBecomeAGoodPrSlvr Aug 09 '17 at 17:13
  • Speaking of the "product" here makes it sounds more clever than necessary. It is just a fancy way of saying "+1 if an even number of them are -1, and -1 otherwise", i.e describing the parity of the number that are -1. The nine chosen points have the property that when you change all signs on a side or diagonal, you change an even number of those chosen points (zero for a side, two for a diagonal). So in all cases the number of -1 chosen points has its parity unchanged - it remains even. 9 is not even, so they can never all become -1. – Nate Eldredge Aug 13 '17 at 06:09
  • So "parity" is always a good sort of invariant to look for. – Nate Eldredge Aug 13 '17 at 06:10
  • @Nate You are absolutely right about the parity part. He could define parity of number of -1s than taking the product. What makes me wonder is that how he was able to isolate the nine points? Invariance based problems have two parts. First is to figure out states in order to form equivalence classes (please refer to https://www.dpmms.cam.ac.uk/~kf262/MMM/L3/L3_1.pdf). Second is to figure out the right function which forms the invariant for each of those equivalence classes. In this problem, the hard part was defining the state. The state here is the set of nine peculiar points. – TryingHardToBecomeAGoodPrSlvr Aug 13 '17 at 16:19
  • Continuing the last comment .... What made me wonder is how on earth did he think of those nine points? Now that I know the solution, it is obvious as to why he chose those nine points. But before that, I could not figure it out. Added to that was my fixation to my own line of thought that I have described in the post. I do not see any obvious connection between my line of thought and the set of those nine points. In general, I am finding it hard to locate either the invariant or the states to form on which we can define "useful" invariants. I wish there were more good books on this topic. – TryingHardToBecomeAGoodPrSlvr Aug 13 '17 at 16:23
  • Well, you can think about it the other way. Knowing that parity is a useful invariant, you can set out to look for an odd set of points that meets any line in an even number of points. Then it's just trial and error. Of course, you will probably try a lot of other invariants before you find the one that works. It only looks clever and ingenious because you don't write down all the things you tried that didn't work. Maybe this will be a lesson not to get "fixated" on one approach. – Nate Eldredge Aug 13 '17 at 16:44
  • You may check Canada's imo training materials – saket kumar Feb 25 '21 at 14:11

2 Answers2

4

Being officially a guy which your are trying hard to become, :-) answering your question I feel obliged to tell you the truth: :-) experience is the best of the teachers. :-) Sometimes you may find a problem solver handbook, helpful for a specific topic, but it won’t be solving problems for you. :-)

Concerning your explicit questions.

1 In order to get better in problem solving matters not the success rate, but level, hardness, depth of problems. Solving thousands of quadratic equations won’t make anybody a good problem solver. :-) On the other hand, I’m solving open problems, so any success rate greater than zero is good for me (then I may publish my solution and to show my boss for what I’m paid :-)).

Of course, IMO level problems are pretty hard. Nevertheless, they should be solved in hours, whereas really hard problems may be solved during decades. My MSE examples: of school level and of professional level). Also parts of this answer may be relevant.

2 Unfortunately, my problem solver handbook knowledge is rather narrow, because I have to solve problems, but not to read how to do this. :-) Also a lot of my problem solving experience is related with old Russian school sources.

As a general problem solver handbooks I may highly recommend George Polya books, especially “Mathematical discovery: on understanding, learning and teaching”. For specific subjects may be useful collections of olympic problems with solutions, grouped into topics. Also you can use tag search at MSE.

Alex Ravsky
  • 106,166
1

From what I hear jj sylvester pretty much invented invariant theory. Maybe take a look at some of his work. He was apparently a pretty good mathematician. .. well, upon looking it up it appears Cayley gets the credit: the idea was suggested to him by an elegant paper of Boole. Here is the wiki. Looking up sylvester, he made fundamental contributions. .. Then again, Encyclopedia brittanica gives credit to both .