Prove that $|z^2+1|\le 2$ implies $|z^3+3z+2|\le 6$

Question

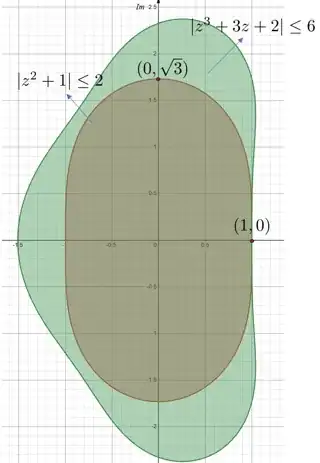
Show that $$\{z \in \mathbb{C}: |z^2+1|\le 2 \} \subseteq \{z \in \mathbb{C} : |z^3+3z+2|\le 6 \} \tag{*}$$ (In other words: Let $z\in \mathbb{C}$ satisfy $|z^2+1|\le 2$. Prove that $|z^3+3z+2|\le 6.$)

This problem was asked by mengdie1982 roughly a day ago(relative to posting this question), but was closed due to lack of work. This has been bothering me because of how simply it has been stated, however even after hours of work I am not close to proving this mathematically. Geometrically the statement (*) is true, as seen below.

$\hspace{4cm}$

Here are some estimates:

1. From reverse triangle inequality, $|z^2+1| \le 2$ implies $|z| \le \sqrt{3}$ with equality at $z=i\sqrt{3}$. From triangle inequality, $|z^3+3z+2| \le |z|^3+3|z|+2 \le 6\sqrt{3}+2 \approx 12.4$. A better bound can also be achieved by factorization, $$|z^3+3z+2| = |z(z^2+1)+2(z+1)| \le |z||z^2+1|+2(|z|+1) \le 4\sqrt{3}+2 \approx 8.93. $$
2. Another approach I took was to show that for any $r<6$, $$\{z \in \mathbb{C}: |z^2+1|\le 2 \} \nsubseteq \{z \in \mathbb{C} : |z^3+3z+2|\le r \} $$ which explains the pinching behavior between the sets near the point $(1,0)$. Define $$L=\left(\frac{2}{2-r+\sqrt{8-4r+r^{2}}}\right)^{\left(\frac{1}{3}\right)},\quad z_0 = \frac{1}{2}\left(1+L-\frac{1}{L}\right), $$ then with much effort, it can be shown that $z_0$ satisfies $|z^2+1|\le 2$, but it is not present in the other set. This implies that (*) can be reworded as finding the largest $r>0$ such that $$\{z \in \mathbb{C}: |z^2+1|\le r \} \subseteq \{z \in \mathbb{C} : |z^3+3z+2|\le 6 \}$$

or it is possible that there is an easier solution which I am missing.

Answer 1

Proof.

Let $z = a + \mathrm{i} b$. It suffices to prove that $$(a^3-3ab^2+3a+2)^2 + (3a^2b-b^3+3b)^2 \le 36$$ for all real numbers $a, b$ with $(a^2-b^2+1)^2 + 4a^2b^2 \le 4$.

We have the following identity \begin{align*} &36-(a^3-3ab^2+3a+2)^2-(3a^2b-b^3+3b)^2\\ ={}& (8a^2+b^2+1)\Big(4-(a^2-b^2+1)^2-4a^2b^2\Big)\\ &\qquad + \frac17(7a^3 + 7ab^2 - 13a + 6)^2 + \frac15(7a^2 + 5b^2 - 7)^2\\ &\qquad + \frac{8}{85}(17a + 12)^2(a - 1)^2 + \frac{60}{119}(a - 1)^2. \end{align*}

We are done.

Answer 2

As River also showed, the implication is equivalent to the following implication involving only real numbers by considering $z = x + iy$:

$$(x^2-y^2+1)^2 + 4x^2y^2 \le 4 \Rightarrow (x^3-3xy^2+3x+2)^2 + (3x^2y-y^3+3y)^2 \le 36. $$

To show the above implication, River nicely used a method based on SOSs, but it requires guessing several functions, which can probably only be done using solvers specifically developed for SOSs and knowing the optimal solution. Here, I prove the above implication using elementary analysis tools.

The above implication can be proven if we show the optimal value $p^*$ of the following optimization problem is less than or equal to 36:

$$\max z(x,y)=A(x,y)^2 + B(x,y)^2 $$ subject to $$(x^2-y^2+1)^2 + 4x^2y^2 \le 4 \tag{1}$$

where

$$A(x,y)=x^3-3xy^2+3x+2, B(x,y)=3x^2y-y^3+3y.$$

Here, we prove $p^*=36$ using the following steps:

1) It can be shown that $ x^2\le 1$. Indeed, from

$$(x^2-y^2+1)^2 + 4x^2y^2 \le 4 \Leftrightarrow (x^2+y^2+1)^2 \le 4(1+y^2), \tag{2}$$

we have $x^2 \le 2\sqrt{1+y^2}-(1+y^2) \le \max_{a}(2a-a^2)= 1.$

2) The equation $\nabla Z(x,y)=0$ is equivalent to

$$(x^2-y^2+1)A(x,y)+2xyB(x,y)=0$$ $$-2xyA(x,y)+(x^2-y^2+1)B(x,y)=0.$$

These together give $$((x^2-y^2+1)^2+4x^2y^2)B(x,y)=0,$$ which has a solution only if $B(x,y)=0 \Leftrightarrow y^2=3(1+x^2) \vee y=0$. The first $y^2=3(1+x^2)$ results in no feasible solution (just plug it into (1)), but $y=0$ yields the feasible solution $(0,0)$ that cannot be optimal (compare it with some trivial feasible solution such as $(1,0)$ or eliminate it at the end of step 3).

3) From step 2, we can see that the optimal value $p^*$ must be attained at some point on the curve $(x^2-y^2+1)^2 + 4x^2y^2 = 4,$ which using (2) can be written as

$$\big (x^2+t(x) \big )^2 = 4t(x), t(x)=y^2+1. $$

Then, $$t(x)=2-x^2+\sqrt{1-x^2}$$ can be explicitly obtained as a function of $x$ by solving the above quadratic equation (it has real roots if and only if $ x^2\le 1$) and noting that $t(x)\ge 1$. As the objective function $z(x,y)$ depends on $y$ through $y^2$, we obtain:

$$ f(x)=\big (x^3-3x(t(x)-1)+3x+2\big)^2+(t(x)-1)\big (3x^2-(t(x)-1)+3 \big)^2\\=\left (4x^3-3x\sqrt{1-x^2}+2 \right)^2 +\left (1-x^2+\sqrt{1-x^2}\right)\left (4x^2-1-\sqrt{1-x^2} \right)^2, |x|\le 1.$$

$f(x)$ [1] is a univariate function of $x$ depicted below [2]:

$\hspace{3cm}$

The maximum is attained at $x=1$, which can be shown by finding the solutions of $f'(x)=0$ [3], which are $r_1=-0.894803$, $r_2=-0.163729$, and $r_3=0.580693$, and then selecting the best among $-1,r_1,r_2,r_3,1$. Therefore, from $t(1)=y^2+1, t(1)=1$, we obtain $y=0$. Hence point $(1,0)$ with $z(1,0)=36$, which also dominates $(0,0)$ obtained in step 2,, is the optimal solution, and thus $p^*=36$. QED

---

Following River's comment, we may be able to prove that the maximum occurs at the boundary without calculus or maximum modulus principle, and the iss to use the transformation $x=\frac{2t}{1+t^2}$ to get rid of $\sqrt{1-x^2}$. The result is given here, which seems complex. I also tried transformation $x=\sin t$, but the result given here is still complex. Any comments are welcome!

Answer 3

Another way.

Let $z = a + \mathrm{i} b$. It suffices to prove that $$(a^3-3ab^2+3a+2)^2 + (3a^2b-b^3+3b)^2 \le 36 \tag{1}$$ for all real numbers $a, b$ with $$(a^2-b^2+1)^2 + 4a^2b^2 \le 4. \tag{2}$$

From (2), we have $4 \ge (a^2 - b^2 + 1)^2 + 4a^2b^2 = (a^2 + b^2 + 1)^2 - 4b^2$ which results in $$a^2 \le 2\sqrt{1 + b^2}- (1 + b^2). \tag{3}$$ Also, by AM-GM, we have $a^2 \le 1 + (1 + b^2) - (1 + b^2) = 1$.(This has been pointed out by @Amir's nice answer.) Also, since $2\sqrt{1+b^2}-(1+b^2)\ge 0$, we have $b^2 \le 3$.

(1) is written as $$(a^3-3ab^2+3a)^2 + 4a(a^2-3b^2+3) + (3a^2b-b^3+3b)^2 \le 32. \tag{4}$$

We split into two cases.

Case 1. $a^2-3b^2+3 > 0$

Using $a^2 \le 1$ and $b^2 \le 3$, we have \begin{align*} &32 - (a^3-3ab^2+3a)^2 - 4a(a^2-3b^2+3) - (3a^2b-b^3+3b)^2\\ \ge{}& 32 - (a^3-3ab^2+3a)^2 - 4(a^2-3b^2+3) - (3a^2b-b^3+3b)^2\\ ={}& -a^6+(-3b^2-6)a^4+(-3b^4-13)a^2-b^6+6b^4+3b^2+20\\ \ge{}& -1+(-3b^2-6)+(-3b^4-13)-b^6+6b^4+3b^2+20\\ ={}& -b^6 + 3b^4\\ \ge{}& 0. \end{align*}

Case 2. $a^2 - 3b^2 + 3 \le 0$

Using $a^2 \le 1$ and $b^2 \le 3$ and (3), we have \begin{align*} &32 - (a^3-3ab^2+3a)^2 - 4a(a^2-3b^2+3) - (3a^2b-b^3+3b)^2\\ \ge{}& 32 - (a^3-3ab^2+3a)^2 + 4(a^2-3b^2+3) - (3a^2b-b^3+3b)^2\\ ={}& -a^6+(-3b^2-6)a^4+(-3b^4-5)a^2-b^6+6b^4-21b^2+44\\ \ge{}& -a^2+(-3b^2-6)a^2+(-3b^4-5)a^2-b^6+6b^4-21b^2+44\\ ={}& -(3b^4+3b^2+12)a^2-b^6+6b^4-21b^2+44\\ \ge{}& -(3b^4+3b^2+12)(2\sqrt{1 + b^2}- (1 + b^2))-b^6+6b^4-21b^2+44\\ \ge{}& -(3b^4+3b^2+12)\left(\frac{2b^2}{1 + b^2/3 + 1} + 2- (1 + b^2)\right)-b^6+6b^4-21b^2+44\\ ={}& \frac{2b^8 + 6b^4 - 112b^2 + 192}{6 + b^2}\\ \ge{}& 0 \end{align*} where we use $\sqrt{1 + b^2} - 1 = \frac{b^2}{\sqrt{1 + b^2} + 1} \le \frac{b^2}{1 + b^2/3 + 1}$ which follows from $$(1 + b^2) - (1 + b^2/3)^2 = \frac19b^2(3-b^2)\ge 0.$$

We are done.

Answer 4

Following some ideas already presented by Amir's answer, assuming wlog $y\ge 0$, we have that

$$|z^2+1|= 2 \implies y=\sqrt{1 - x^2 + 2 \sqrt{1 - x^2}} \tag 1$$

with $|x|\le 1$, then we need to prove that $|z^3+3z+2|^2-36\le 0 $ that is

$$ F(x,y)=((2 + 3 x + x^3 - 3 x y^2)^2 + (3 y + 3 x^2 y - y^3)^2)-36\le 0 \tag 2$$

and by substituting $(1)$ in $(2)$ we obtain

$$f(x)=4 (-1 + 6 x^2 + 4 x^3 + 2 \sqrt{1 - x^2} (1 - 3 x + 2 x^2))-36\le 0$$

and by $x=\sin u$ with $u\in\left[-\frac \pi 2, \frac \pi 2\right]$ we obtain

$$f(u)=8 (-1 + \sin u) (6 - \cos u - \cos(2 u) + 5 \sin u + \sin(2 u)) \le 0$$

which reduces the given problem $(2)$ to prove that

$$g(u)=6 + 5 \sin u + \sin(2 u)- \cos u - \cos(2 u) \ge 0 \tag 3$$

which is indeed true and can be proved as indicated here below.

---

Proof of $(3)$

(deleted, refer to the following alternative proof)

---

Alternative and clever proof of $(3)$

As shown by River Li's answer here, we simply have

$$g(u)=6 + 5 \sin u + \sin(2 u)- \cos u - \cos(2 u) \ge $$

$$\ge 6 + 5 \sin u -1- 1 - (1-2\sin^2 u)=$$

$$=3+ 5 \sin u+2\sin^2 u= (2\sin u + 3)(\sin u + 1)\ge 0$$