Crux problem #33 with vector approach

Question

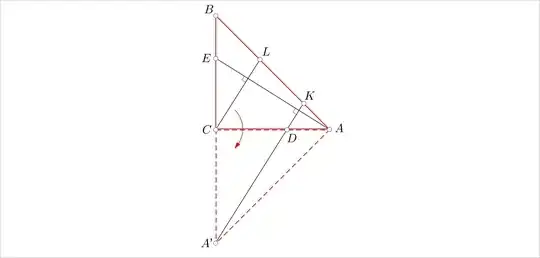
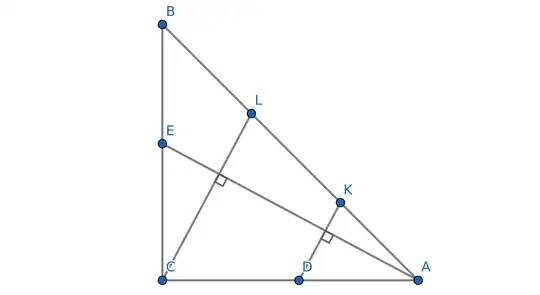
On the sides $CA$ and $CB$ of an isosceles right-angled triangle $ABC$, points $D$ and $E$ are chosen such that $|CD|=|CE|$. The perpendiculars from $D$ and $C$ on $AE$ intersect the hypotenuse $AB$ in $K$ and $L$ respectively. Prove that $|KL|=|LB|$.

Proposed by Victors Linis, University of Ottawa.
Crux Mathematicorum Vol. 1, No. 4, June, 1975

I want a solution via vectors and I'll explain why in the end of the question, tl;dr.
The question consists of:

• the basic things we can do with vectors,
• how did I come to a regular geometric solution,
• regular geometric solution,
• motivation for vectors approach.

---

To give more explicit context, I'll explain the basic things we can do with vectors to approach real geometry problems.

1. We can add or subtract vectors, e.g. $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$.
2. We can scale a vector by a coefficient (say $k$) so if $A,B,C$ lie on the same line and $k=\frac{AC}{AB}$ then $\overrightarrow{AC}=k\overrightarrow{AB}$.
3. In particular, 1. and 2. follows that if $X$ is on $AB$, such that $\frac{AX}{XB}=\frac{t}{1-t}$ then $\overrightarrow{OX}$ $=\overrightarrow{OA}+\overrightarrow{AX}$ $= \overrightarrow{OA}+t\,\overrightarrow{AB}$ $= \overrightarrow{OA}+t(\overrightarrow{OB}-\overrightarrow{OA})$$= t\,\overrightarrow{OB}+(1-t)\,\overrightarrow{OA}$.
4. If some vectors form a basis, then every vector has unique representation as a linear combination of basis vectors with coefficients called "coordinates" (e.g. $\overrightarrow{i},\,\overrightarrow{j},\,\overrightarrow{k}$ is a classical basis for 3d Cartesian coordinates).
   Knowing only 1.-4. some problems like this (not in a way attention drawing) may be solved when a convinient basis is chosen, and even Ceva's_theorem, Menelaus's theorem, Thales' theorem can be proven, almost in an algebraic way. I'd call such "linear vector problems". But we know also
5. Scalar (dot) product. By definition $\cos\angle BAC=\frac{\overrightarrow{BA}\cdot\overrightarrow{BC}}{ |\overrightarrow{BA}|\cdot|\overrightarrow{BC}|}$, or, alternatively, $(\overrightarrow{BA}\cdot\overrightarrow{BC})=BA\cdot BC\cdot \cos\angle BAC$. This implies such things like $(\overrightarrow{BA}\cdot \overrightarrow{BA})=(\overrightarrow{BA})^2=|\overrightarrow{BA}|^2=BA^2$ and $(\overrightarrow{BA}\cdot\overrightarrow{BC})=0\Leftrightarrow BA\perp BC$ unless $BA$ or $BC$ equals to zero. All distributive laws holds for addition/subtraction related to scalar or/and dot product.
   With 1.-5. such things like cosine rule, Heron's formula, Ptolemy's_theorem can be proven and I believe the problem above can be solved too.) We also know (though it's usage mostly limited by 3d Cartesian space)
6. Cross product

Having these tools, we can approach problems, where all conditions given and things to be proven/found are: parallelity, perpendicularity, fixed angles, intersection, intersection at a ratio (and maybe some others). But apparently we can't deal with circles, addition/subtraction of angles and many other things. But boiling a geometric problem down to algebra can be useful when no other ways seen. Other approaches are complex numbers or Cartesian coordinates, but vectors are unfairly less popular/known. I'd say, many vectors excercises are constructed just to train using vectors, instead of showing how real geometrical problems may be solved in an algebraic way.

---

Arriving at regular geometrical solution

I made the figure above in geogebra and started moving free point $D$ back and forth and see how the things change and I noted that somewhat asymmethrical that we have $3$ points on $AB$ and only two on $AE$, I wanted inverse-image of $B$ to be present to. To construct it, I mirrored $B$ relative to $AE$ into $B'$.

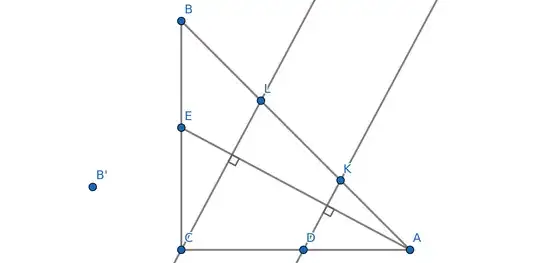
By moving $D$ I noted that $BB'||CL||DK$ (and indeed, they all are perpendicular to $AE$) and that reminded me of Thales' theorem -- if we have say $F=BB'\cap AC$

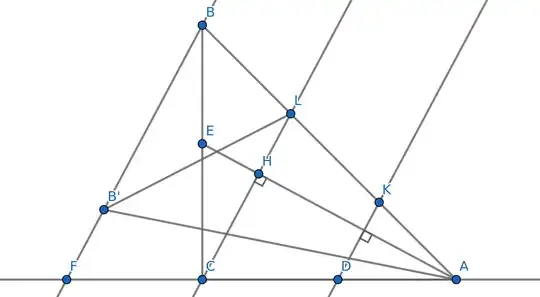
then it would suffice to show that $DC=CF$ and use Thales' theorem. By "method of gazely staring" I found that $\triangle CFB\sim \triangle HEC$, but it's obvious that $\triangle HEC\sim\triangle CEA$, but $CA=CB$ and thus $CE=CF$, but it's given that $CD=CE$, which completes the proof.

---

Geometrical solution, refined

We take $F$ on the line $AC$ such that $BF||CL$.
$\angle FBC=\angle ECH$, where $H=CL\cap EA$.
From right-angled $\triangle ECH$: $\angle ECH=90^\circ -\angle CEH$,
but from right-angled $\triangle ECA$: $\angle CAE=90^\circ -\angle CEH$
thus $\angle FBC=\angle ECH=\angle EAC$
hence $\triangle FBC$ and $\triangle EAC$ are congruent by ASA
that follows $CF=CE$,
but it's given that $CD=CE$ thus $CF=CD$
and using Thales' theorem on lines $AB$, $AC$ intersected by $BF \parallel CL \parallel DK$ we obtain $BL=LK$, QED.

---

But imagine I were at a contest without being able to use geogebra and move the point $D$ and to want to construct $BB'$, then arriving at this solution with such additional constructions is highly doubtful. While vectors approach is pretty straightforward: algebraically express what's given and what's needed, solve algebraical problem, usually a linear equations system. That's why I want vectors solution. Other algebraical solutions, like Cartesian coordinates, complex coordinates or even something like barycentric coordinates are welcome as well.

Thanks for reading this through out.)

Answer 1

Rotate the triangle $ABC$ clockwise $90^\circ$ around the point $C$. Then $A$ goes into $A'\!\in \ C\vee B$, and $E$ into $D$. From the following figure it is evident that $|KL|=|LB|$.

Answer 2

$\def\vec{\overrightarrow}\def\R{\mathbb{R}}$Because $K, L, B$ are collinear and $K ≠ B$ (see Remark), there exists $t \in \mathbb{R}$ such that$$ \vec{AL} = t \vec{AK} + (1 - t) \vec{AB}, $$ so\begin{gather*} \vec{AL} · \vec{AE} = t \vec{AK} · \vec{AE} + (1 - t) \vec{AB} · \vec{AE}. \tag{1} \end{gather*} Note that $DK \perp AE$, thus$$ 0 = \vec{DK} · \vec{AE} = (\vec{AK} - \vec{AD}) · \vec{AE} \Longrightarrow \vec{AK} · \vec{AE} = \vec{AD} · \vec{AE}. $$ Analogously, $CL \perp AE$ implies that $\vec{AL} · \vec{AE} = \vec{AC} · \vec{AE}$. Therfore (1) implies that\begin{gather*} \vec{AC} · \vec{AE} = t \vec{AD} · \vec{AE} + (1 - t) \vec{AB} · \vec{AE}. \tag{2} \end{gather*} Since $\vec{CE} = s \vec{CB}$ and $\vec{AD} = (1 - s) \vec{AC}$, where $s = \dfrac{CE}{CB} = \dfrac{DC}{AC}$, then $AC \perp CB$ implies that\begin{gather*} \vec{AC} · \vec{AE} = \vec{AC} · (\vec{AC} + s \vec{CB}) = |\vec{AC}|^2,\\ \vec{AD} · \vec{AE} = (1 - s) \vec{AC} · (\vec{AC} + s \vec{CB}) = (1 - s) |\vec{AC}|^2,\\ \vec{AB} · \vec{AE} = (\vec{AC} + \vec{CB}) · (\vec{AC} + s \vec{CB}) = |\vec{AC}|^2 + s |\vec{CB}|^2 = (1 + s) |\vec{AC}|^2. \end{gather*} Plugging into (2) yields $1 = t(1 - s) + (1 - t)(1 + s) = 1 + (1 - 2t)s$, combining with $s ≠ 0$ yields $t = \dfrac{1}{2}$. Therefore $L$ is the midpoint of $BK$ and $|KL| = |LB|$.

---

Remark: If $K = B$, then $DB \perp AE$. However,\begin{gather*} \vec{DB} · \vec{AE} = (\vec{DC} + \vec{CB}) · (\vec{AC} + \vec{CE})\\ = \vec{DC} · \vec{AC} + \vec{CB} · \vec{CE} = s \vec{AC} · \vec{AC} + \vec{CB} · s \vec{CB} = 2s |\vec{AC}|^2 ≠ 0, \end{gather*} a contradiction.

Answer 3

I would provide an additional rapid solution, strictly based on analytical geometry. Let us scale and place our triangle in a Cartesian plane, with vertices in points $C(0,0)$, $B(0,1)$, $A(1,0)$.

The hypothenuse $AC$ lies on the line $y=-x+1$. If we set $\overline{CD}=\overline{CE}=k$, the slope of $AE$ is $-k$. Then the equation of the line containing $AE$ is $y=-kx+k$. Since $AL$ and $DK$ are perpendicular to $AE$, their slope is $1/k$. So $AL$ is on the line $y=x/k$ and $DK$ is on the line $y=x/k-1$. Now, by the standard method to find the intersection point of two lines, we get $$L\left(\frac{k}{k+1}, \frac{1}{k+1}\right)$$

$$K\left(\frac{2k}{k+1}, \frac{1-k}{k+1}\right)$$

This directly shows that both the $x$- and $y$-coordinates of the points $B$, $L$, and $K$ are in arithmetic progression, thus completing the proof.

Answer 4

So I've come to a vectors solution myself, though it was not so hard.
Let $a:=\overrightarrow{CA},\,b:=\overrightarrow{CB},\, \overrightarrow{CD}=xa,\,\overrightarrow{CE}=yb$. It's given that $$\overrightarrow{CL}=ua+(1-u)b,\, \overrightarrow{CK}=va+(1-v)b,\,\\ \overrightarrow{CL}\cdot(a-yb)=0,\, \overrightarrow{DK}\cdot(a-yb)=0,\,ab=0.$$ $$\begin{cases} (ua+(1-u)b)\cdot(a-yb)=0\\ (va+(1-v)b-xa)\cdot(a-yb)=0 \end{cases}$$ $$\begin{cases} ua^2-(1-u)yb^2=0\\ (v-x)a^2-(1-v)yb^2=0 \end{cases}$$ $$\begin{cases} u(a^2+yb^2)=yb^2\\ v(a^2+yb^2)=xa^2+yb^2 \end{cases}$$ $$\frac{BK}{BL}=\frac{v}{u}=\frac{xa^2+yb^2}{yb^2}$$ And when $x=y,\,a^2=b^2$ $\quad \frac{BK}{BL}=2$, QED. However, it does not seem to be able to derive $\cot$ from this.
Looking back at the solution length it looks more a vector excercise than a real problem. I wonder why this method appeared inaccessable for $<10k$ reputation MSE community members.

Answer 5

Notations:

• vectors are in bold ($\bf{ca}$ goes from point C to point A); '$\times$' denotes a cross product
• $\bf{u}$ is a unit vector going into the page; $\bf{o}$ is the zero vector

Problem definition:

• ${\bf{cb}}=({\bf{ca}} \times \bf{u})$

• ${\bf{cd}}=y \, {\bf{ca}}$ and ${\bf{ce}}=y \, {\bf{cb}}$, for some parameter y

• $\bf{cl}$ and $\bf{dk}$ orthogonal to $\bf{ae}$ means ${\bf{cl}}=z ({\bf{ae}} \times {\bf{uv}})$ and ${\bf{dk}}=w ({\bf{ae}} \times {\bf{uv}})$, for some $z$ and $w$

• By construction, ${\bf{bl}} = m \, {\bf{lk}}$ for some unknown scalar $m$

Proof: (that $m=1$, independently of $y$)

• ${\bf{lk}}.{\bf{ae}} = (-{\bf{cl}}+{\bf{cd}}+{\bf{dk}}).{\bf{ae}}$

  $\, \, \,= {\bf{cd}}.{\bf{ae}}$, since $({\bf{ae}} \times {\bf{uv)}}.{\bf{ae}} = {\bf{o}}$

  $\, \, \,= y \, {\bf{ca}}.{\bf{ae}} = y \, {\bf{ca}}.{\bf{(ac}}+{\bf{ce}})$

  $\, \, \,= -y \, {\bf{ca}}.{\bf{ca}}$, since ${\bf{ce}} = y \, {\bf{cb}} = y \, ({\bf{ca}} \times {\bf{u}})$ and ${\bf{ca}}.({\bf{ca}} \times {\bf{u}})={\bf{o}}$

• ${\bf{bl}}.{\bf{ae}} = (-{\bf{cb}}+{\bf{cl}}).{\bf{ae}}$

  $\, \, \, = -{\bf{cb}}.{\bf{ae}}$, since $({\bf{ae}} \times {\bf{uv}}).{\bf{ae}} ={\bf{o}}$

  $\, \, \, = -{\bf{cb}}.(-{\bf{ca}}+{\bf{ce}})$

  $\, \, \, = -y \, {\bf{cb}}.{\bf{cb}}=-y \, ({\bf{ca}} \times \bf{u}).({\bf{ca}} \times \bf{u})$

  $\, \, \, = -y \, {\bf{ca}}.{\bf{ca}}$

• But since ${\bf{bl}} = m \, {\bf{lk}}$, one also has ${\bf{bl}}.{\bf{ae}} = m \, {\bf{lk}}.{\bf{ae}}$ and therefore $m=1$, i.e. ${\bf{bl}} = {\bf{lk}}$.

Notes:

• There is no condition on the sign of $y$ or on its norm being smaller than 1. So, the proof is also valid if both C and D are on the prolongation of the edges (provided that their 'sign', i.e. their side of C compared to their edge, is consistent).
• There is a geometric interpretation for the steps of the vectorial proof, e.g. the projections of ${\bf{lk}}$ and ${\bf{cd}}$ on ${\bf{ae}}$ are identical, etc. I think that brings something.
• Also, all these equivalent geometric operations stay 'within the triangle'.

Answer 6

Put the origin of a Cartesian coordinate system to $C$, direct axis along the sides $CA$ and $CB$ such that coordinates of points $A$ and $B$ are $(1,0)$ and $(0,1)$, respectively. Then there exists $0\le a\le 1$ such that coordinates of points $D$ and $E$ are $(a,0)$ and $(0,a)$ (according to the picture, I assumed that the point $D$ belongs to $CA$ and the point $E$ belongs to $CB$). Also $K=(k,1-k)$ and $L=(\ell,1-\ell)$ for some $k,\ell$. Since $(\ell,1-\ell)=CL \perp EA=(1,-a)$, we have the inner product $(CL,EA)= \ell-(1-\ell)a=0$, so $\ell=\tfrac a{a+1}$ and $|LB|=\sqrt{2}\ell=\sqrt{2}\tfrac a{a+1}$. Since $(k-a,1-k)=DK \perp EA$, we have $(DK,EA)=(k-a)-(1-k)a=0$, so $k=\tfrac {2a}{a+1}$ and $|KL|=\sqrt{2}(k-\ell)=\sqrt{2}\tfrac a{a+1}=|LB|$.

PS.

approach is pretty straightforward: algebraically express what's given and what's needed, solve algebraic problem.

This is an idea of the Cartesian program to solve problems. As some other his clear ideas, it turned out to be too naїve. See its development in a book "Mathematical discovery: on understanding, learning and teaching" by George Polya (in Russian translation "Математическое открытие" Джорджа Пойа), which is helpful for contest problem solvers.

Differences between analytical and geometrical approaches to geometrical problems were considered by an adept of the first approach, V. Tikhomirov in a paper “Geometry or analysis” (in Russian) from the good old “Kvant”, which I read when I was a schoolboy.

I was good in school algebra and weak in school geometry so at contests I first quickly solved algebraic problems and postponed geometrical those to end. Then I had some time left for a one or two problems and usually used an analytical approach to solve them. At a contest, when a quick solution is needed and a search for geometrical tricks like an additional construction can be fruitless, this was a good strategy for me. Nevertheless, sometimes an analytical way can lead to cumbersome calculations and be too long, whereas an easy trick can shorten a solution a lot. Once I had a problem to calculate some angle, which I finally did, canceling cumbersome fractions. Later I got to know that the other contestants simply drew a picture, measured that angle and proved that it is equal to fifteen degrees. So I lost a lot of time due to my straightforward approach. This could cost me a few points, which was crucial for me, because this contest was an IMO selection and I turned out a few points below my main competitor from my city, and he was qualified to be in the team, whereas I was not (luckily for me, he obtained no awards at that IMO, so the head of our school thought that if I would participated instead of my competitor then I could win an award, but this is an other story).

Another example of a long analytical way to an answer is my solution of this bounty geometry problem, which was even not upvoted although it was the first.

Sometimes an analytical way can be too complicated and lead to a blind alley, for instance, when I studied an inequality from celestial mechanics, see these comments.

Answer 7

Let's prove a generalization for arbitrary right triangles. The algebra is slightly hairier than the isosceles case, but the end result seems worth the extra effort.

---

Consider $A=(a,0)$, $B=(0,b)$, $C=(0,0)$, $A'=(0,a')$, $B'=(b',0)$. (My $A'$ and $B'$ play the roles of OP's $D$ and $E$.)

Define $$K := \dfrac{A+k B}{1+k}= \frac1{1+k}\left(a,bk\right) \tag{1}$$ If $\overline{AA'}\perp\overline{B'K}$, then $$\begin{align} 0=(K-B')\cdot(A-A') &\sim \left(a-b'-b'k,bk\right)\cdot (a,-a') \tag{2}\\[4pt] &= a(a-b')-(ab'+a'b) k \tag{3} \end{align}$$ so that $$k = \frac{a(a-b')}{ab'+a'b}\quad\to\quad K = \frac1{a^2+a'b}\left(a(ab'+a'b),ab(a-b')\right) \tag{4}$$ Next, define $$L := \dfrac{K+\ell B}{1+\ell} = \frac{1}{(a^2+a'b)(1+\ell)}\left(a(ab'+a'b),b\left(a(a-b')+(a^2+a'b)\ell\right)\right) \tag{5}$$ If $\overline{AA'}\perp CL$, then

$$\begin{align} 0 = (L-C)\cdot(A-A') &\sim a^2(ab'+a'b)-a'b(a(a-b')+(a^2+a'b)\ell) \tag{6}\\[4pt] &=(a^2+a'b)\left( ab'-a'b\ell\right) \tag{7} \end{align}$$ Therefore,

$$\frac{|KL|}{|LB|} = \ell = \frac{ab'}{a'b} = \frac{a/b}{a'/b'}=\frac{\cot A}{\cot A'} \tag{$\star$}$$

In the particular problem with two isosceles triangles, $\cot A = \cot A'=1$, so that $(\star)$ shows $L$ to be the midpoint of $\overline{KB}$. Note that $L$ is also the midpoint for not-necessarily-isosceles but appropriately-similar right triangles. $\square$

---

Vectors aside, here's a straightforward geometric proof:

$$\frac{|KL|}{|LB|}=\frac{|UV|}{|VW|}=\frac{|OB'|\cos\theta}{|OB|\sin\theta}=\frac{|OB'|}{|OB|}\frac{|OA|}{|OA'|}=\frac{\cot A}{\cot A'}$$