Trapezium, transversals...and a median?

Question

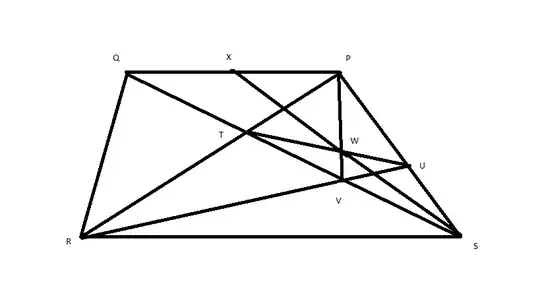
$PQRS$ is a trapezium with bases $PQ$ and $RS$. $T$ is the point where diagonals $PR$ and $QS$ intercept. $U$ is a point located in side $SP$. $V$ is the point where $QS$ and $RU$ intercept. $W$ is the point where $PV$ and $TU$ intercept. $X$ is the point where $SW$ and $PQ$ intercept.

Is $X$ the middle of $QP$?

Is <span class= $X$ middle of $QP$?" />

Likely Ceva's or Menelaus's theorems would help. Vectors approach is certainly the way to go. — Alexey Burdin, Aug 15 '20 at 17:41
Yes, $X$ is the middle of $PQ$ for arbitrary $U$, WA vectors proof here (see h->1/2). — Alexey Burdin, Aug 15 '20 at 18:05

score 2 · Accepted Answer · answered Aug 15 '20 at 18:51

2

The Euclidean Geometry way:

Menelaus: ${TR\over PR}\cdot{PU\over SU}\cdot{SV\over TV} = 1$

Ceva: ${TY\over PY}\cdot{PU\over SU}\cdot{SV\over TV} = 1$

Therefore ${TR\over PR}={TY\over PY}$

Draw $PZ$ parallel to $QS$ intersecting $SX$ at $Z$.

Now ${TR\over PR}={TS\over QS}$, ${TY\over PY}={TS\over PZ}$

Therefore $QS=PZ$ and $PSQZ$ is a parallelogram. Therefore $QX=XP$.

answered Aug 15 '20 at 18:51

cr001

12,778

1

Nice a cute answer. – MrDudulex Aug 15 '20 at 19:04

Trapezium, transversals...and a median?

1 Answers1