0

I have two line segments that are perpendicular to each other and intersect. I want to know the point of intersection, given one endpoint of one segment and both endpoints of the other. I also know that the other endpoint of the first segment lies on the second segment (and therefore is the point of intersection).

Thaddaeus Markle
  • 175

2 Answers2

0

You know that one is perpendicular to the other. So if you have the two endpoints of one line you can calculate its slope. Then you can calculate the slope of the other line as well (because it is perpendicular to the first). Then use point slope form to get two equations for the two lines and solve the system of equations for their intersection.

Please let me know if there is something I can clarify :)

atul ganju
  • 996
  • Thanks for your answer! Just a few questions...it's been too long since I did math ;-). Would you mind reminding me what point-slope form is? Also, these lines are graphics as part of a computer program, so using the equation of the lines is a little tricky. Is there a formula I could just plug a few numbers into instead? Thanks again. – Thaddaeus Markle Jul 20 '20 at 15:32
  • Sure. Lets define the slope of a line as $b$ and a point we know the line goes through as $a = (a_x, a_y)$. Then point slope is as follows: $(y-a_y) = b(x-a_x)$. – atul ganju Jul 20 '20 at 15:35
  • You can use this formula for point slope (and the formula for slope) to develop a formula for the intersection! Again lmk if you have any questions :) – atul ganju Jul 20 '20 at 15:36
  • Could you just edit your answer to step through the process (similar to what Alexey did)? – Thaddaeus Markle Jul 20 '20 at 15:59
  • I have no idea what he's doing, but I like how he structured his answer better than you did. :-) – Thaddaeus Markle Jul 20 '20 at 16:00
0

Let $\mathbf{b},\,\mathbf{c}$ be the known endpoints of segment and $\mathbf{a}$ be the known endpoint of the other segment.
For a point $\mathbf{x}$ on the first segment we have $\mathbf{x}=t\mathbf{b}+(1-t)\mathbf{c}$ (see here, point 3. why).
And we have $$(\mathbf{x}-\mathbf{a})\cdot (\mathbf{b}-\mathbf{c})=0$$ $$(t\mathbf{b}+(1-t)\mathbf{c}-\mathbf{a})\cdot (\mathbf{b}-\mathbf{c})=0$$ $$t(\mathbf{b}-\mathbf{c})^2+(\mathbf{c}-\mathbf{a})\cdot (\mathbf{b}-\mathbf{c})=0$$ $$t= \frac{(\mathbf{a}-\mathbf{c})\cdot (\mathbf{b}-\mathbf{c})}{ (\mathbf{b}-\mathbf{c})^2}$$ And thus $$\mathbf{x}=\mathbf{c}+ \frac{(\mathbf{a}-\mathbf{c})\cdot (\mathbf{b}-\mathbf{c})}{ (\mathbf{b}-\mathbf{c})^2}(\mathbf{b}-\mathbf{c})$$

Okay, geometrical intuition behind the answer for the case pure vectors don't make sense:

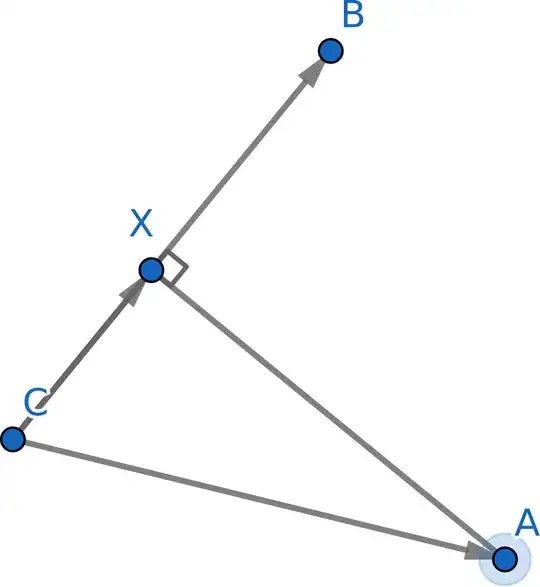
$\overrightarrow{CX}=\mathbf{x}-\mathbf{c}$ is the normed vector $\overrightarrow{CB}=\mathbf{b}-\mathbf{c}$ (i.e. $\frac{\mathbf{b}-\mathbf{c}}{|\mathbf{b}-\mathbf{c}|}$) multiplied by the length of projection $\overrightarrow{CA}$ onto $\overrightarrow{CB}$.
The length of projection is $$|\overrightarrow{CA}|\cos\angle ACB= |\overrightarrow{CA}| \frac{\overrightarrow{CA}\cdot\overrightarrow{CB}}{ |\overrightarrow{CA}|\cdot|\overrightarrow{CB}|}= \frac{\overrightarrow{CA}\cdot\overrightarrow{CB}}{ |\overrightarrow{CB}|}$$ so the overall result is $$\mathbf{x}-\mathbf{c}= \frac{(\mathbf{a}-\mathbf{c})\cdot(\mathbf{b}-\mathbf{c})}{|\mathbf{b}-\mathbf{c}|} \cdot \frac{\mathbf{b}-\mathbf{c}}{|\mathbf{b}-\mathbf{c}|}$$

Alexey Burdin
  • 5,299
  • Sorry, maybe it's just me, but reading your answer I'm completely lost... What is t? And why are you solving for x? – Thaddaeus Markle Jul 20 '20 at 16:09
  • "I have two line segments that are perpendicular to each other and intersect. I want to know the point of intersection, given one endpoint of one segment ($\mathbf{a}$) and both endpoints of the other ($\mathbf{b},,\mathbf{c}$). I also know that the other endpoint of the first segment ($\mathbf{x}$) lies on the second segment" so it's the only unknown, and we find it, i.e. solving for it. – Alexey Burdin Jul 20 '20 at 16:15
  • Ok, I understand a little better now, but how does solving for x give you the coordinates for the point x? Sorry, I haven't learned about vectors yet. – Thaddaeus Markle Jul 20 '20 at 16:16
  • You may think I simply denoted $\mathbf{x}=(x_X,y_X)$ along with $\mathbf{a}=(x_A,y_A)$, $\mathbf{b}=(x_B,y_B)$, $\mathbf{c}=(x_C,y_C)$. Vectors are added/subtracted component-wise, e.g. $\mathbf{a}-\mathbf{c}=(x_A-x_C,y_A-y_C)$ and the scalar product $(a,b)\cdot(c,d)$ is $ac+bd$ in cartesian coordinates. Multiplying by a scalar is component-wise too. – Alexey Burdin Jul 20 '20 at 16:23
  • So it's just a more convinient notation for $$(x_X,y_X)=(x_C,y_C)+\frac{(x_A-x_C)(x_B-x_C)+(y_A-y_C)(y_B-y_C)}{(x_B-x_C)^2+(y_B-y_C)^2}(x_B-x_C,y_B-y_C)$$ More, in higher-dimensional Cartesian spaces the result will be the same, except for there will be more coordinates (such as $z$ for 3d). – Alexey Burdin Jul 20 '20 at 16:27
  • Ok, I got it now, I think. I'll try this out. – Thaddaeus Markle Jul 20 '20 at 16:30
  • Let us continue this discussion in chat. – Thaddaeus Markle Jul 20 '20 at 16:31