1

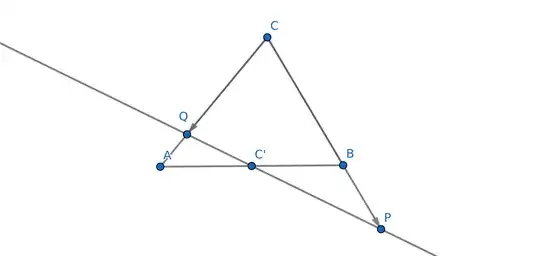
I am given a triangle $ABC$ with the points $P, Q$ on the plane of the triangle such that:

$$\overrightarrow{PC} = \dfrac{3}{2} \overrightarrow{BC} \hspace{2cm} \overrightarrow{AQ} = \dfrac{1}{4} \overrightarrow{AC}$$

I have to show that the points $P, Q$ and $C'$ (where $C'$ is the midpoint of the segment $[AB]$) are colinear. I seem to be a bit lost. Firstly I drew the picture, it looks like this. I hope the link works, I never drew a triangle online before. Here's an image of it, in case the GeoGebra link doesn't work.

From my understanding, in order to show that two vectors $\overrightarrow{a}$ and $\overrightarrow{b}$ are colinear I have to show that there is a relation:

$$\overrightarrow{a} = k \cdot \overrightarrow{b}$$

where $k \in \mathbb{R}$. So I tried finding such a relation using two of the vectors $\overrightarrow{PQ}, \overrightarrow{PC'}$ and $\overrightarrow{C'Q}$, but I couldn't find it. (By the way, is that condition enough? It seems to me that the condition would be satisfied even if the two vectors would be parallel and the points of the vectors are certainly not colinear if they are parallel. Is there another condition that needs to be satisfied?)

I took into consideration the fact that in the first part of the problem I had to express the vector $\overrightarrow{PQ}$ in terms of the vectors $\overrightarrow{AB}$ and $\overrightarrow{AC}$. After a lot of manipulation and trial and error, I got the expression:

$$\overrightarrow{PQ} = \dfrac{3}{4} \overrightarrow{AC} - \dfrac{3}{2} \overrightarrow{AB}$$

I thought that the subpoints of the problem are somehow related so I can use this expression to find out thtat $P,Q$ and $C'$ are colinear but I didn't get anywhere. I kept transforming vectors and expressing them as a sum of two other vectors over and over again, starting from the beginning a few times but still couldn't find the solution.

This is how I approached all of these types of problems with vectors so far. Just trial and error, which seems to fail me this time. Is there a more general approach that I could follow, or do I just keep trying to express vectors as sums and differences of other vectors until I get the desired result? That doesn't seem to work this time, or at least I didn't get to the solution yet.

2 Answers2

1

Hint: Use Menelaus theorem for triangle $ABC$ and point $Q, C', P$

From the relations given we conclude that $\frac{CQ}{QA}\times\frac{AC'}{C'B}\times\frac{BP}{PC}=\frac{3}{1}\times\frac{1}{1}\times\frac{0.5}{1.5}=1$. Therefore by Menelaus Theorem points $P, Q$ and $C'$ are colinear.

Daniyar Aubekerov
  • 953
  • 1
    That was way easier than expected, I just didn't get that idea. Thank you so much! –  Jan 19 '20 at 15:21
  • 1
    No worries, you can also check Ceva's Theorem, which is also usually helpful in that type of question! And don't forget to upvote my answer, haha! – Daniyar Aubekerov Jan 19 '20 at 15:25
  • 1
    @DabiyarAubekerov Can you please explain when does Menelaus's Theorem equate the ratios with $1$ and when does it equate the ratios with $-1$? I am looking at this theorem online and some sources are with $-1$ while others are with $1$. –  Jan 19 '20 at 15:33
  • 1
    Technically it is correct to say -1, because in vector form (when in you undecided about exact positions of these points) we use $-1$. But for the picture you attached using Menelaus theorem with segments I mentioned above, it will be just $1$. – Daniyar Aubekerov Jan 19 '20 at 15:43
0

It's clear that it's worth to take $C$ as the origin as we're given $\overrightarrow{CP}=\frac32\overrightarrow{CB}$, $\overrightarrow{CQ}=\frac34\overrightarrow{CA}$,
so let $a=\overrightarrow{CA},\,b=\overrightarrow{CB}$, then for every point $X$ on the line $PQ$ we have $\overrightarrow{CX}=t\,\overrightarrow{CP}+(1-t)\,\overrightarrow{CQ}$ for some $t$ (see here point 3. why).
Now we find $\overrightarrow{CC'}=\frac{\overrightarrow{CA}+\overrightarrow{CB}}{2}=\frac{a+b}{2}$ and see if we can find some $t$ for $\overrightarrow{CC'}=\frac32 tb+\frac34(1-t) a$. If we find such $t$, this proves that $C'$ is on the line $PQ$, if it's not on the line, we will not ba able to find such $t$.
As $a,\,b$ forms a basis we have (see the link above point 4. why) $$ \begin{cases} \frac32 t=\frac12\\ \frac34 (1-t)=\frac 12 \end{cases} $$ $t=\frac{1}{3}$ fits into both equations, we have $\overrightarrow{CC'}=\frac13\,\overrightarrow{CP}+(1-\frac13)\,\overrightarrow{CQ}$ so $C'$ is on the line $PQ$, QED.

Alexey Burdin
  • 5,299