Point $A$ lies on the perpendicular bisector of $BC$. $M$ and $N$ are points respectively in line segments $AB$ and $AC$ such that $MN$ is tangent to the incircle of $ABC$ at point $H$. $MP, NQ \perp BC$ ($P,Q \in BC$). The intersection of $MQ$ and $NP$ is point $K$. Prove that $HK$ passes through a fixed point.
It's the midpoint of $BC$, obviously, but how to prove it is more important, which I failed to do. This problem is adapted from a recent competition.
Ignoring vertex $A$, this becomes a problem on the inscriptable $\square BCNM$. Let $L$ be the midpoint of $\overline{BC}$. Also, let $M'$ (instead of $P$), $N'$ (instead of $Q$), $H'$, $K'$ be the projections of $M$, $N$, $H$, $K$ onto $\overline{BC}$. Let the tangent segments from $B$ and $C$ to the incircle have length $d$; let the tangent segments from $M$ and $N$ have length $m$ and $n$. Finally, define $m' := |MM'|$, $n':=|NN'|$, $m'':=|M'L|$, $n'':=|N'L|$. Without loss of generality, $m\leq n$ so that $m'\leq n'$.
Certainly, if $m=n$, then $\overleftrightarrow{HK}$ meets $\overline{BC}$ at $L$. For $m \neq n$, we'll prove that $L$ is on $\overleftrightarrow{HK}$ by showing $\triangle HH'L\sim \triangle KK'L$ via $$|HH'||K'L|=|KK'||H'L| \tag{$\star$}$$
Parallelism and proportionality rules tell us that $$\frac{|M'H'|}{|M'N'|}=\frac{|MH|}{|MN|}=\frac{m}{m+n} \qquad |HH'|=m'+\frac{m}{m+n}(n'-m')=\frac{m'n+mn'}{m+n} \tag{1}$$ The Crossed Ladders Theorem tells us that $$\frac{1}{|KK'|}=\frac{1}{m'}+\frac{1}{n'} \quad\to\quad |KK'| = \frac{m'n'}{m'+n'} \tag{2}$$ (and, in fact, $K$ is the midpoint of the extension of $\overline{KK'}$ that meets $\overline{MN}$), whereupon some proportional thinking then yields $|M'K'|:|K'N'|=m':n'$, so that we have $$\frac{|M'K'|}{|M'N'|}=\frac{m'}{m'+n'} \tag{3}$$ Therefore, $$\begin{align} |H'L|&=|M'L|-|M'H'| = m'' - \,\frac{m}{m+n}(m''+n'') \;= \frac{m''n-mn''}{m+n} \\[6pt] |K'L|&=|M'L|-|M'K'| = m'' - \frac{m'}{m'+n'}(m''+n'')=\frac{m''n'-m'n''}{m'+n'} \end{align} \tag{4}$$ Substituting in $(\star)$, and clearing denominators, we need only verify that $$(m'n+mn')(m''n'-m'n'') = m'n'(m''n-mn'') \tag{5} $$ That is, $$\frac{m}{n}\cdot\frac{m''}{n''} = \left(\frac{m'}{n'}\right)^2 \tag{6}$$
It seems like there's a geometric mean argument to be made, but I'm not seeing it. So, writing $\theta$ for the common angle at $B$ and $C$, we have $$\frac{m}{n}\cdot\frac{d-(m+d)\cos\theta}{d-(n+d)\cos\theta} = \left(\frac{m+d}{n+d}\right)^2 \quad\to\quad (d+m)(d+n)\cos\theta = d^2 - m n \tag{7}$$ This same relation results (for $\theta \neq 0$) from the observation that there's a right triangle with hypotenuse $|MN|$ and legs $|m'-n'|$ and $m''+n''$. $$(m+n)^2 = (m'-n')^2 + (m''+n'')^2 \qquad\to\qquad (7) \tag{8}$$ This equality establishes $(\star)$ and completes the proof. $\square$
I believe there's a cleaner way to link $(6)$ and $(8)$ (or to demonstrate $(6)$ some other way) without having to show equality through $(7)$. Again, I'm not seeing it. Perhaps I'll return to this question.
Here's a quicker way to relation $(7)$ from my previous answer.
Reiterating the setup from the previuos answer: Ignoring $A$, this is a problem on inscriptable $\square BCNM$. Let $L$ be the midpoint of $\overline{BC}$, and let $M'$ and $N'$ be the projections of $M$ and $N$ onto $\overline{BC}$. Let the tangential segments from $B$ and $C$ to the incircle have length $d$, let the tangential segments from $M$ and $N$ have lengths $m$ and $n$, and let define $m':=|MM'|$ and $n':=|NN'|$. We may assume $m\leq n$ so that $m'\leq n'$.
If $m=n$, then clearly $\overleftrightarrow{HK}$ contains $L$. For $m\neq n$, let the extensions of $\overline{BC}$ and $\overline{MN}$ meet at $X$. We'll prove collinearity of $H$, $K$, $L$ using Menelaus' Theorem, verifying this product:
$$\left[\frac{XL}{LM'}\right] \cdot \left[\frac{M'K}{KN}\right]\cdot\left[\frac{NH}{HX}\right] \stackrel{?}{=} -1 \tag{$\star$}$$ where "$[\frac{PQ}{RS}]$" indicates a signed ratio of lengths $|PQ|$ and $|RS|$: the sign is positive if $\overrightarrow{PQ}$ and $\overrightarrow{RS}$ point the same way, and negative if they point opposite ways. In the configuration shown, betweenness guarantees that the product of the signed ratios will be negative, as desired; therefore, we'll simplify things by proving absolute-value version of the relation: $$\frac{|XL|}{|LM'|} \cdot \frac{|M'K|}{|KN|}\cdot \frac{|NH|}{|HX|} \stackrel{?}{=} 1 \tag{$\star\star$}$$ Since $\overline{XL}$ and $\overline{HX}$ are tangent segments from $X$, they are congruent: $$|XL|=|HX| \tag{1}$$ Since $\triangle MM'K\sim\triangle N'NK$ and $\triangle MM'B\sim \triangle NN'C$ we have $$\frac{|M'K|}{|KN|}=\frac{m'}{n'}=\frac{m+d}{n+d} \tag{2}$$ Finally, we clearly have $$|NH|=n \qquad\text{and}\qquad |LM'| = d - (m+d)\cos\theta \tag{3}$$ Substituting $(1)$, $(2)$, $(3)$ into $(\star\star)$ gives
$$\frac{1}{d-(m+d)\cos\theta} \cdot\frac{m+d}{n+d} \cdot\frac{n}{1} \stackrel{?}{=} 1 \qquad\to\qquad d^2-mn \stackrel{?}{=} (m+d)(n+d)\cos\theta \tag{4}$$
This is relation $(7)$ from the previous answer. As shown there, the equality holds due to a Pythagorean relation that I won't repeat here (because I removed a few of the relevant lengths from the figure). Thus, we have $(\star\star)$, which implies that $H$, $K$, $L$ are indeed collinear. $\square$
Note. $H$ can actually be anywhere on the incircle (barring degeneracies). The reader is invited to adapt the above argument accordingly; that said, a coordinate-based proof, albeit computationally cumbersome, can be performed that is completely agnostic as to the position of $H$.
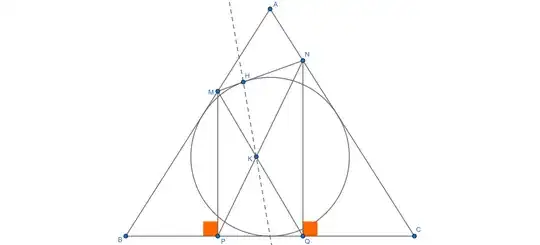
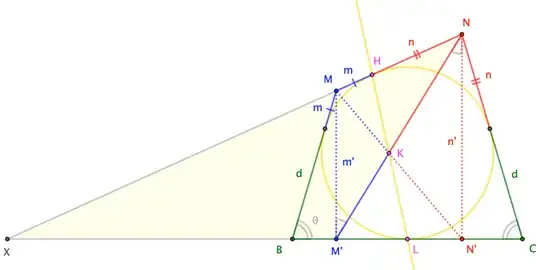
We can analytically prove that the straight line spanned by $HK$ passes through the midpoint of $BC$ as follows. Let the side $BC$ of the triangle lies along $x$-axis, and the origin $O$ is the midpoint of $BC$. Let ther vertex $A$ is a point $(0,a)$ and the vertices $B$ and $C$ are points $(-b,0)$ and $(b,0)$ respectively ($a,b>0$). Let $I=(0,r)$ be the center of the incircle and $H=(x_h,y_h)=I+r(\cos\varphi,\sin\varphi)$. Let $R$ (resp. $S$) be the tangent point of the incircle to the side $AB$ (resp. $AC$) of the triangle $ABC$. Since the point $H$ belongs to the upper arc of the incircle spanned by the points $R$ and $S$, $\theta\le\varphi\le\pi-\vartheta$, where $\tan\theta=\tfrac ba$. Let $M=(m,h_m)$, $P=(0,h_m)$, $N=(n,h_n)$, $Q=(0,h_n)$. Collinearity of points $A$, $B$, and $M$ implies $h_m=a\left(\tfrac {m}{b}+1\right)$. Similarly, collinearity of points $A$, $C$, and $N$ implies $h_n=a\left(\tfrac {-n}{b}+1\right)$. Let $K=(x_k,y_k)$. Similarity of triangles $KMP$ and $KQN$ implies $\tfrac{x_k-m}{h_m}=\tfrac{n-x_k}{h_n}$, so $x_k=\tfrac {nh_m+mh_n}{h_m+h_n}.$ Considering an angle $NPQ$, we obtain $\tfrac{x_k-m}{y_k}=\tfrac{|PQ|}{|NQ|}=\tfrac{n-m}{h_n}$. Thus $$y_k=\frac {h_n(x_k-m)}{n-m}=\frac{h_n}{n-m}\left(\frac {nh_m+mh_n}{h_m+h_n}-m\right)=\frac {h_mh_n}{h_m+h_n}.$$ It remains to show that the points $O$, $K$, and $H$ are collinear, that is $$\frac{b}{a}\left(\frac{n}{b-n}+\frac{m}{m+b}\right)= \frac{n}{h_n}+\frac{m}{h_m}=\frac{x_k}{y_k}=\frac{x_h}{y_h}=\tfrac{\cos\varphi}{1+\sin\varphi}.$$ Since $MH\perp IH$ we have
$(r\cos\varphi-m)r\cos\varphi+\left(r(1+\sin\varphi)- a\left(\tfrac {m}{b}+1\right)\right)r\sin\varphi =0$
$(r\cos\varphi-m)\cos\varphi+\left(r(1+\sin\varphi)- a\left(\tfrac {m}{b}+1\right)\right)\sin\varphi =0$
$br-bm\cos\varphi+rb\sin\varphi-am\sin\varphi-ab\sin\varphi=0$
If $ b\cos\varphi+ a\sin\varphi =0$ then $HI\perp AB$, so $H=R$. Then $N=A$, so $Q=O$ and formally $M$ can be any point of $AB$. But in order to have the straight line spanned by $HK$ passes through $O$, we restrict ourselves to $M=R$ in this case. Then $H=M$ and $K$ belongs to $MO$.
Below we shall assume that $a\sin\varphi+ b\cos\varphi \ne 0$. Then
$m=b\frac{r(1+\sin\varphi)-a\sin\varphi }{b\cos\varphi+ a\sin\varphi}.$
It follows
$\frac{m}{m+b}=1-\frac{ a\sin\varphi+ b\cos\varphi}{b\cos\varphi+ r(1+\sin\varphi)}.$
Similarly, since $NH\perp IH$ we have
$(r\cos\varphi-n)r\cos\varphi+\left(r(1+\sin\varphi)-a\left(\tfrac{-n}{b}+1\right)\right)r\sin\varphi =0$
$br-bn\cos\varphi+rb\sin\varphi+an\sin\varphi-ab\sin\varphi=0$
If $b\cos\varphi-a\sin\varphi=0$ then $HI\perp AC$, so $H=S$. Then $M=A$, so $P=O$ and formally $N$ can be any point of $AC$. But in order to have the straight line spanned by $HK$ passes through $O$, we restrict ourselves to $M=S$ in this case. Then $H=M$ and $K$ belongs to $NO$.
Below we shall assume that $b\cos\varphi-a\sin\varphi\ne 0$. Then
$n=b\frac{r(1+\sin\varphi) -a\sin\varphi}{b\cos\varphi-a\sin\varphi }.$
It follows
$\frac{n}{b-n}=-1+\frac{b\cos\varphi-a\sin\varphi }{b\cos\varphi-r(1+\sin\varphi)}.$
Thus
$\frac{m}{m+b}+\frac{n}{b-n}=\frac{b\cos\varphi-a\sin\varphi }{b\cos\varphi-r(1+\sin\varphi)}- \frac{ a\sin\varphi+ b\cos\varphi}{b\cos\varphi+ r(1+\sin\varphi)}=$
$\frac{2b\cos\varphi(r(1+\sin\varphi)-a\sin\varphi)}{b^2\cos^2\varphi-r^2(1+\sin\varphi)^2}$.
So it remains to verify that
$\frac ba\frac{2b\cos\varphi(r(1+\sin\varphi)-a\sin\varphi)}{b^2\cos^2\varphi-r^2(1+\sin\varphi)^2}=\frac{\cos\varphi}{1+\sin\varphi}$
It suffices to check that
$\frac{2b^2(r(1+\sin\varphi)-a\sin\varphi)}{b^2\cos^2\varphi-r^2(1+\sin\varphi)^2}=\frac{a}{1+\sin\varphi}$
$\frac{2b^2(r(1+\sin\varphi)-a\sin\varphi)}{b^2(1+\sin\varphi)(1-\sin\varphi)-r^2(1+\sin\varphi)^2}=\frac{a}{1+\sin\varphi}$
$2b^2(r(1+\sin\varphi)-a\sin\varphi)=a(b^2(1-\sin\varphi)-r^2(1+\sin\varphi))$
$(2b^2r-ab^2+ar^2)(1-\sin\varphi)=0$
That is, we need to show that $2b^2r-ab^2+ar^2=0$. That is $r=\tfrac{-2b^2\pm \sqrt{4b^4+4a^2b^2}}{2a}=\tfrac{-b^2\pm b\sqrt{b^2+a^2}}{a}$. Indeed, the radius $r$ equals the area $ab$ of the triangle $ABC$ divided by its semiperimeter $b+\sqrt{a^2+b^2}$. It follows $r=\frac ba\left(\sqrt{a^2+b^2}-b \right)$.
