In which ratio does the point $P$ divide the segment $\overline{AN}$?

Question

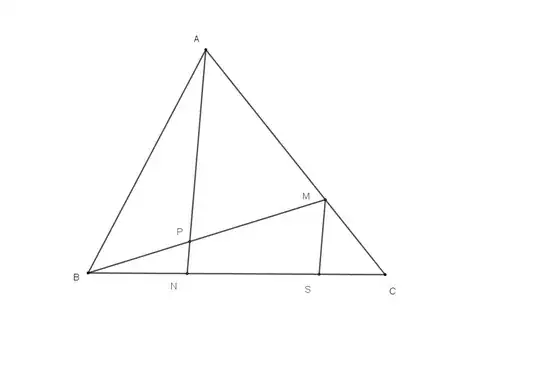
In an arbitrary triangle $\triangle ABC$, let $M\in\overline{AC}$ s. t. $|AM|:|MC|=2:1$ and let $N\in\overline{BC}$ s. t. $|BN|:|NC|=1:2$. Let $P$ be the intersection point of the segments $\overline{AN}$ and $\overline{BM}$. In which ratio does the point $P$ divide the segment $\overline{AN}$?

---

My attempt:

I thought I could apply the intercept theorem to find the ratio in which the point $P$ divides the segment $\overline{BM}$ and then express $\overrightarrow{AP}$ as a linear combination of $\overrightarrow{BM}$ and some vector in $\triangle ABC$ linearly independent of $\overrightarrow{BM}$.

Let $S\in\overline{NC}$ s. t. $\overline{AN}\parallel\overline{MS}$. From the given ratios, it follows: $|AM|=2\lambda,\ |MC|=\lambda,\ |BN|=\mu, |NC|=2\mu, \ \lambda,\mu\in\Bbb Q$. By the intercept theorem, $$\begin{aligned}&|SC|:|NS|=|MC|:|AM|=1:2\\\implies&|SC|=\nu,\ |NS|=2\nu,\ \nu\in\Bbb Q\\\implies&|NC|=|NS|+|SC|=3\nu=2\mu\implies\mu=\frac32\nu\end{aligned}$$ Then $$\begin{aligned}&|BP|:|PM|=|BN|:|NS|=\frac{\mu}{2\nu}=\frac{\frac32\nu}{2\nu}=\frac34\\\implies&\overrightarrow{PM}=\frac47\overrightarrow{BP}=\frac47\left(\frac13\overrightarrow{AC}-\overrightarrow{BC}\right)\end{aligned}$$ but it doesn't seem I've accomplished anything by finding $\frac{|BP|}{|PM|}.$ It would be perfect if I could find $\frac{|AP|}{|PN|}$ the same way, but there isn't enough information to do that and compare that result with $\overrightarrow{AP}=\alpha\left(\overrightarrow{AC}-\overrightarrow{NC}\right),\ \alpha\in\Bbb Q$. Another option was to consider a midpoint $T$ of the segment $\overline{NC}$, so $\overrightarrow{BT}=\frac23\overrightarrow{BC}$. Then $$\overrightarrow{AP}=\alpha\left(\overrightarrow{AB}+\overrightarrow{AT}\right)$$ May I ask for advice on solving this task?

Thank you in advance!

Answer 1

I will use vectors too, so a picture is redundant.
Let $\overrightarrow{CA}=a,\,\overrightarrow{CB}=b$ and $C$ be the origin.
Then $M=\frac{1}{3}a,\,N=\frac{2}{3}b$, $$P\in AN:\quad P=uA+(1-u)N=ua+\frac{2}{3}(1-u)b,$$ $$P\in BM:\quad P=vB+(1-v)M=vb+\frac{1}{3}(1-v)a,$$ $$\hbox{as }P=ua+\frac{2}{3}(1-u)b=vb+\frac{1}{3}(1-v)a$$ and $a,\,b$ forms a basis, then $$\begin{cases} u=\frac{1}{3}(1-v)\\ v=\frac{2}{3}(1-u) \end{cases}$$ $$\begin{cases} u=\frac{1}{7}\\ v=\frac{4}{7} \end{cases}$$ $$\hbox{So }\frac{AP}{PN}=\frac{1-u}{u}=6.$$

Answer 2

Let $\mathcal{H}_{X,k}$ denote a homothety with center at $X$ and a extension factor $k$.

We have a following fact (Theorem):

If $\mathcal{H}_{X,k_1}$ and $\mathcal{H}_{Y,k_2}$ are homotheties then their compostion $\mathcal{H}_{X,k_1}\circ \mathcal{H}_{Y,k_2}$ is again some homothety $\mathcal{H}_{S,k}$ with $k=k_1k_2$ (if $k\ne 1$) and it center $S$ lies on a line $XY$.

Since we have: \begin{align} \mathcal{H}_{M, {-2}}: & \;C \longmapsto A\\ \mathcal{H}_{B,{3}}: &\; N \longmapsto C\\ \end{align} we see that $P$ is a center of homothety which takes $N$ to $A$ with ratio $-6$, so $AP:PN = 6:1$.