Find the border radius tangent's relative coordinates in a rhombus

Question

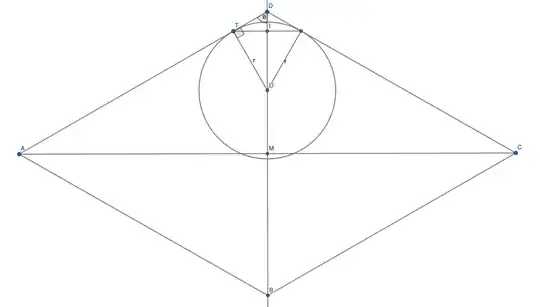
I have this rhombus. The width w and height h, and the coordinates of M the intersection of the diagonals is also given. The border radius r is given.

Notice how the circle with center O and radius r is tangent to the segments [AD] in the point T.

In this diagram, $w = AC$ and $h = BD$, so they are interchangeable below.

I want to find the coordinates of the point T, the intersection point between the border radius circle and the side of the rhombus, relative to M.

So I need a way to express the distance TI and the distance IM only in terms of w, h, and r.

(finding IM is the same as finding DI, since $IM=\frac{w}{2}-DI$)

There are four right angle triangles of interest:

• TDO
• ADM
• TDI
• TIO

Here are the equations I have obtained inside each triangle:

Triangle TDO

$\cos(\theta)=\frac{DT}{DO}$

$\sin(\theta)=\frac{r}{DO}$

$\tan(\theta)=\frac{r}{DT}$

$DO^{2}=DT^{2}+r^{2}$

Triangle ADM

$\tan(\theta)=\frac{w}{h}$

Triangle TDI

$\cos(\theta)=\frac{DI}{DT}$

$\sin(\theta)=\frac{TI}{DT}$

$\tan(\theta)=\frac{TI}{DI}$

$DT^{2}=DI^{2}+TI^{2}$

Triangle TIO

$\cos(\theta)=\frac{TI}{r}$

$\sin(\theta)=\frac{IO}{r}$

$\tan(\theta)=\frac{IO}{TI}$

$r^{2}=TI^{2}+IO^{2}$

There's no system of equations solver online willing to solve this, and I am unsure how to proceed to solve for the unknowns TI and IM in terms of the knowns w, h, and r.

Answer 1

Consider this as a comment. Someone willing to convert it to an answer can do it.
Let $M=(0,0),\,D=(0,\frac y2),\, C=(\frac x2,0)$ where I use $x,y$ instead of $w,h$.
$T$ being on the line $CD$ is $T=tC+(1-t)D$ and $O$ being on the line $MD$ is $O=sD$.
We have $$(O-T)\cdot (C-D)=0,\ (O-T)^2=r^2,$$ solving this yields $$T=\left(\pm\frac{ry}{\sqrt{x^2 + y^2}}, \frac y2 \left(1 \mp \frac{2ry}{x\sqrt{x^2 + y^2}}\right) \right)$$