Recurrence with varying coefficient

Question

Problem 1

$$ {\rm f}\left(n\right) = \frac{1}{n}\, \left[{\rm f}\left(n - 1\right)k_{0} + {\rm f}\left(n-2\right)k_{1}\right]\tag{1} $$

( This can also be written as ${\rm Q}\left(n\right) = k_{0}\frac{{\rm Q}\left(n - 1\right)}{n - 1} +k_{1}\frac{{\rm Q}\left(n - 2\right)}{n - 2}$ provided ${\rm Q}\left(n\right) = n{\rm f}\left(n\right) $ )

where $k_{0},\,k_{1}$ are constants. ${\rm f}\left(0\right)=3,\,{\rm f}\left(1\right)=5$. The variable coefficient $\frac{1}{n}$ is making lot of issues here. It blocks the proper expansion.

Question

Please help me to find the solution of the recurrence in terms of $n$ ( implies ${\rm f}\left(n\right)$ ) and also the summation of the recurrence up to infinity ( $ sum = \sum_{n = 0}^{\infty}{\rm f}\left(n\right)$ ).

Note::

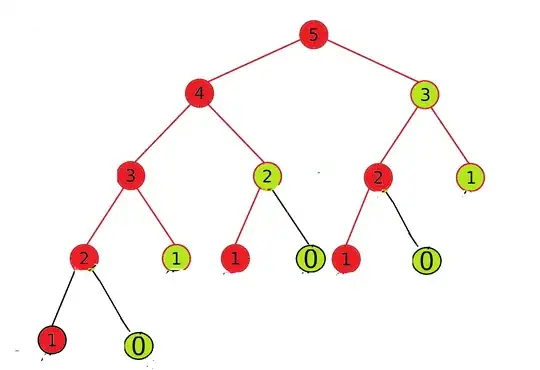
1. Partial answers are also welcome. We can discuss that here. This recursion forms a structure of Fibonacci look like tree. I have attached a pic here. You can see Red nodes to indicate $k_0$ multiplication and green to indicate $k_1$ multiplication. You can see the index of the tree expands like a Fibonacci sequence(starts from 5)

2. Some of the generating function smart manipulations can be looked in to this famous e book for reference link:-generatingfunctionology!

3. I know a method of using ODE. But I am trying to solve it with out ODE so that I can extent this to higher dimension like matrices in similar structure questions. Please avoid ODE solution or any matrix exponential. A method using series would be more desirable
   

Problem 2( extended Matrix version of problem 1)

We have a given matrix recurrence ,

$ (\curlyvee_i,\curlyvee_{i-1})_{1\times2}= (\curlyvee_{i-2},\curlyvee_{i-3})_{1\times2}{\begin{bmatrix}A_{i-1}A_i+B_i & A_{i-1} \\B_{i-1}A_i & B_{i-1} \end{bmatrix}}_{2\times2} \tag 1$

$A_i= r\frac{\Im1}{i},B_i= r^2\frac{\Im2}{i} \tag 2$

$ \Im1=\left( \begin{array}{ccc} 0 & -n_0 & m_0 \\ n_0 & 0 & -l_0 \\ -m_0 & l_0 & 0 \\ \end{array} \right), \Im2=\left( \begin{array}{ccc} 0 & -(n_1-n_0) & (m_1-m_0) \\ (n_1-n_0) & 0 & -(l_1-l_0) \\ -(m_1-m_0) & (l_1-l_0) & 0 \\ \end{array} \right).\tag3$

$l_1,m_1,n_1,l_0,m_0,n_0,r$ all are constants can't alter at all

Given Data about the problem

1. Dimensions of $A_i,B_i,\curlyvee_i$ are $3\times3$ and $A_i,B_i$ are skew symmetric matrices with diagonal zero
2. Our initial condition is given as $(\curlyvee_1,\curlyvee_{0})_{1\times3} $

3. Properties of $\Im1,\Im2$ useful for simplification are given below

   For each matrices $\Im1 ( a=l_0,b=m_0,c=n_0), \Im2 ( a=l_1-l_0,b=m_1-m_0,c=n_1-n_0)$,let $p = \sqrt{a^2+b^2+c^2}$. It is true that $\wp^3 = -(a^2+b^2+c^2)\wp = -p^2\wp$ ($\wp$ represents matrices $\Im1, \Im1$ ,select a,b,c accordingly). Hence, $\wp^{2m+1} = (-1)^mp^{2m}\wp \tag 4$ and $\wp^{2m} = (-1)^{m-1}p^{2m-2}\wp^2 \tag 5$. In essence it says both matrices $\Im1, \Im2$ satisfies this property. courtesy @JimmyK4542

Question 1. How do we solve this recurrence in terms of n. Is there any way to take out n from the $3\times3$ matrices in recursion so that we can go for easy simplification. ?

NB :: I would like to have a solution with out using ODE or matrix exponential as I can extent to tensors etc. Please avoid such solution. Those were discussed earlier. Another version of the same question I posted as graph problem is given here. I didnt get any response to that,so I made it simplified as matrix recursion here. I haven been trying lot of methods on it none is successful coz of the properties of $A_i$

Note :: Bounty will be awarded to the helpful suggestions which leads to solution.

Efforts done so far

1. Tried to evaluate using power series simple method. Result:: failed ,Reason :: varying n blocks the procedure
2. Tried to make another equivalent series by substitution. Result :: failed,Reason :: it still went back to old issues. (not sure any nice substitution exists such that we can get form that is solvable..trying)
3. Made it as graph problem .I see a finite structure in Tree and node coloring.. If we go with graph theory method to get an expression for general case n and later add all as series up to infinity , we can find a sequence some thing like GP. We may end up in a finite expression. Result :: Failed ,Reason:: It was tough to get that common expression for a graph based on node contribution
4. Made it as matrix recursion, Result :: failed, could not decompose the matrix recursion component to separate n
5. Tried to compare or extract some properties from Fibonacci tree as it has same structure. Result :: Failed,Reason:: we will still end up in varying coefficient ..

Answer 1

So I do realize you wanted to avoid a matrix exponential answer, now I would like to post one here just so other people running into this question can see what that looks like:

$$ \textbf{MATRIX SOLUTION}$$

Let: $$L(f(n)) = f(n) - f(n-1)$$ Notice therefore:

$$L^2(f(n)) = f(n) - 2f(n-1) + f(n-2)$$

Therefore we can re-write as

$$f(n) = \frac{k_1}{n}(L^2 (f(n)) - 2L(f(n)) + f(n)) + \frac{k_0}{n}(f(n) - L(f(n)))$$

use $f = f(n)$ for cleaner appearance and use standard operator notation (no parenthesis between L and f)

$$f = \frac{k_1}{n}(L^2 f - 2Lf + f) + \frac{k_0}{n}(f - Lf)$$

Which simplifies to

$$\frac{k_1}{n}L^2f + \left(-\frac{2k_1+k_0}{n}\right)Lf + \left(\frac{k_0 + k_1 - n}{n} \right)f = 0 $$

We now multiply through by $n$ and divide by $k_1$

$$L^2f - \left(\frac{2k_1+k_0}{k_1}\right)Lf + \left(\frac{k_0 + k_1 - n}{k_1} \right)f = 0 $$

And move all terms besides $L^2f$ to the other side

$$L^2f = \left(\frac{2k_1+k_0}{k_1}\right)Lf - \left(\frac{k_0 + k_1 - n}{k_1} \right)f $$

Now generate a vector $G = \begin{bmatrix} f \\ Lf \end{bmatrix} $

At this point it becomes evident that if we define $L$ to act component by component on matrices then:

$$LG = \begin{bmatrix} - \frac{k_0 + k_1 - n}{k_1} && 0 \\ 0 && \frac{2k_1 + k_0}{k_1} \end{bmatrix}G$$

Traditionally to solve equations of the type

$$Lf = bf$$

exploits the fact that

$$L(2^{Q(n)}) = (2^{LQ(n)}-1)2^{Q(n)}$$

In other words we are seeking a matrix $H$ such that

$$ 2^{LH(n)} - I_2 = \begin{bmatrix} - \frac{k_0 + k_1 - n}{k_1} && 0 \\ 0 && \frac{2k_1 + k_0}{k_1} \end{bmatrix}$$

Meaning

$$2^{LH(n)} = \begin{bmatrix} - \frac{k_0 - n}{k_1} && 0 \\ 0 && \frac{3k_1 + k_0}{k_1} \end{bmatrix} $$

At this point we must find the components of:

$$\log_2 \left( \begin{bmatrix} - \frac{k_0 - n}{k_1} && 0 \\ 0 && \frac{3k_1 + k_0}{k_1} \end{bmatrix} \right) $$

This is a tricky calculation which requires we replace the 0 components with a variable z. Then compute the logarithm treating, z as a real variable. Then for each component $c_i$ solve

$$Lu = c_i$$

to assemble the components of $H(n)$

from here

$$2^{H(n)}$$

will be the solution of the system

And therefore the dot product of the top row of $2^{H(n)}$ with the vector $\begin{bmatrix} c_0 \\ c_1 \end{bmatrix}$ is the general solution to our problem

At this point take the limit as $z \rightarrow 0$ to recover the solution

$$ \textbf{SERIES SOLUTION} $$

We note that given the linear operator described above

$$Lf = f(n) - f(n-1)$$

We can generate a Taylor-like series by first observing the existence of a product rule

$$L(f*g) = f(n)g(n) - f(n-1)g(n-1) = g*Lf + f*Lg - Lg*Lf $$

And second observing that

$$L \left( \frac{1}{n!} \prod_{i=1}^{n}{(x +i-1)}\right) =\frac{1}{n!} \prod_{i=1}^{n-1}{(x+i-1)} $$

Thereby allowing us to generate a "series"

$$f(x) = f(a) + Lf(a)x + \frac{L^2f(a)}{2!}x(x+1) + \frac{L^3f(a)}{3!}x(x+1)(x+2)... $$

We now recall the original problem:

$$L^2f = \left(\frac{2k_1+k_0}{k_1}\right)Lf - \left(\frac{k_0 + k_1 - n}{k_1} \right)f $$

We can consider the values of

$$ \begin{matrix} L^2f && L^3f && L^4f && ... && L^rf \end{matrix}$$

At which point it becomes evident

$$ L^rf = \left(2 + \frac{k_0}{k_1}\right)L^{r-1}f + \frac{r-2}{k_1}L^{r-3}f + \left(\frac{n}{k_1} - 1 - k_0+ \frac{r-2}{k_1} \right)L^{r-2}f$$

This can be re-written by noting $L^rf = X(r)$ and therefore

$$X(r) = aX(r-1) + (r-2)bX(r-3)+ (c + b(r-2))X(r-2)$$

Whereas $X(0) = 3, \ X(1) = (5-3) = 2$ and $$a = \left(2 + \frac{k_0}{k_1}\right), \ b = \frac{1}{k_1}, \ c = \left(\frac{n}{k_1} - 1 - k_0 \right) $$

Now the solution to the problem is

$$f(n) = \sum_{i=0}^{\infty} \left[ \frac{X(i)}{i!} \prod_{j=1}^{i} (n + j - 1) \right]$$

$$ f(n) = X(0) + X(1)n + \frac{X(2)}{2}n(n+1) + \frac{X(3)}{3!}n(n+1)(n+2) ... $$

Of course finding a closed form for $X$ seems to be a still intriguing problem but not impossible since it is of the exact same form as the original problem: we can create a matrix solution or series solution for $X$ (depending on personal preference...) but to address the concerns of dividing by $k_0$ and $k_1$ our solution terms can instead be written as:

$$ k_1*L^rf = \left(2k_1 + k_0\right)L^{r-1}f + (r-2)L^{r-3}f + \left(n - k_1 - k_0*k_1+ (r-2) \right)L^{r-2}f$$

Thus we can still attempt to solve for each individual $L^{r}f$ and generate series terms... I am curious how this will play out and whether any inconsistent systems will be formed (if they are formed: does that mean there cannot exist a solution to said equation, or does it require the creating of a new flavor of functions outside of all others, much like how we can create an imaginary constant to deal with the unsolvable $\sqrt{-1}$ problem)

Answer 2

Let we set $a_n=f(n)$, and $$ g(x) = \sum_{n=0}^{+\infty} a_n x^n.$$ Since: $$ x\cdot g'(x) = \sum_{n=1}^{+\infty} n\, a_n x^{n},$$ $$ x\cdot g(x) = \sum_{n=1}^{+\infty} a_{n-1} x^{n},$$ $$ x^2\cdot g(x) = \sum_{n=2}^{+\infty} a_{n-2} x^{n},$$ the recursion gives that $g(z)$ is a solution of the differential equation: $$ x\cdot g'(x)-5x = k_0(x\cdot g(x)-3x)+k_1 x^2\cdot g(x), $$ i.e: $$ g'(x) = (k_0+k_1x)g(x)+(5-3k_0),$$ with the constraint $g(0)=3$. Assuming that the inhomogeneous part does not affect really much the behaviour of the coefficients of the Taylor series, we have: $$ a_n\approx [x^n]e^{k_0 x+\frac{k_1}{2}x^2} = \sum_{j=0}^{\lfloor n/2\rfloor}\frac{k_0^{n-2j}k_1^{2j}}{4^j j!(n-2j)!},$$ and $$\sum a_n = g(1)\leq C\cdot e^{k_0+\frac{k_1}{2}}.$$

Answer 3

We can rewrite it as

$-( f(n-1)) =\{k_1f(n-3)+k_1f(n-3)n+k_1f(n-3)n^2+k_1f(n-3)n^3+..+\infty\}+\{k_0f(n-2)+k_0f(n-2)n+k_0f(n-2)n^2+k_0f(n-2)n^3+..+\infty\}\tag1$

from $-f(n-1)=\frac{1}{1-n}(k_0f(n-2)+k_1f(n-3))\tag 2$.Taking summation up to infinity in n from both ends we get the terms involving $\sum_{n=0}^{\infty} f(n)$ on both sides. But some infinite terms on RHS will still exist. We need some smart ways to tackle it with existing infinite series with known finite sum. What is your take guys..Please share

NB :: Have a look at some existing series a) example series 1 ! b) example series 2-page 52 !

NB:: I am now thinking about converting it to another series so that can tackle it better(something like $K(n)=nf(n-1)$,just thinking only..;))