Tree Traversal - Simple Puzzle type Issue.

Question

This is a puzzle like question,based on Fibonacci like structure of the tree. Actually it is a short question with out any complex concepts. It appears bit big,since I have added explanations with example to avoid confusion. Compared to Fibonacci tree structure,our tree has node zero also added, that is the only minor difference. Basically aim is to utilize the Fibonacci Tree properties. I have been trying this more than one week. For understanding, I have given the example of a Fibonacci like tree pic with $n=5 $ for our case. If you check the node index, you can identity the Fibonacci indexing

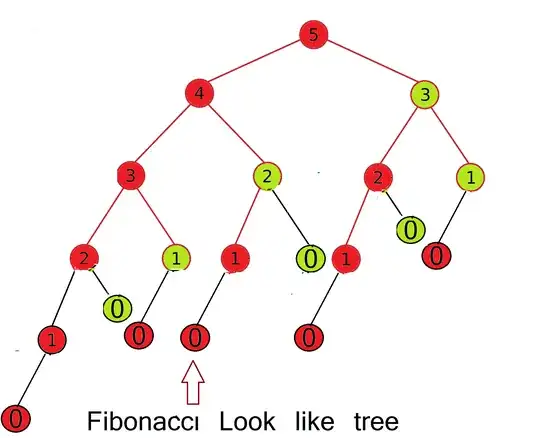
Given data about the Tree for the Puzzle Question

1. Each node has an Index as indicated in the figure. Leaf Index is $0$
2. Each node is colored such that left child from each is colored Red and Right child is colored Green
3. Each node, except tree root, has a Scalar Weight Value associated with it, let us call it as SWV(n). It is calculated as $\frac{1}{P(n)}$. Where $P(n)$ will give the index number of the parent node of current node n. For example $SWV(4)=\frac{1}{5}$

4. Each node, except tree root, has a Matrix Weight Value attached with it. Let us call it $MWV_1,MWV_2$,where $MWV_1(n)=SWV(n)*S_1$ and $MWV_2(n)=SWV(n)*S_2$. Values of $S_1$ and $S_2$ are simple and is given below. If the node is Red, it is given by $MWV_1(n)$ and if it is green, it is given by $MWV_2(n)$. Example, node 4 in the pic has $MWV_1(4)=\frac{1}{5}S_1$ and node 2 has $MWV_2(2)=\frac{1}{4}S_2$(child of node 4)

   $$S_1=\left( \begin{array}{ccc} 0 & -c_0 & b_0 \\ c_0 & 0 & -a_0 \\ -b_0 & a_0 & 0 \\ \end{array} \right).$$ $$S_2=\left( \begin{array}{ccc} 0 & -(c_1-c_0) & (b_1-b_0) \\ (c_1-c_0) & 0 & -(a_1-a_0) \\ -(b_1-b_0) & (a_1-a_0) & 0 \\ \end{array} \right).$$

   NB: All entries of the matrices $S_1$, $S_2$ are constants,can't be altered

   Some properties of $S_1$ and $S_2$ extracted from Given conditions as hints

   a) $S_2$ can be written in-terms of of $S_1$ and a constant matrix made of $a_1,b_1,c_1$

   b) Both are skew symmetric matrices with diagonals $0$

   c) $p = \sqrt{a_0^2+b_0^2+c_0^2}$, $S_1 ^3 = -(a_0^2+b_0^2+c_0^2)S_1 = -p^2 S_1$. Hence, $S_1^{2m+1} = (-1)^mp^{2m}S_1$ and $S^{2m} = (-1)^{m-1}p^{2m-2}S_1^2$ (courtesy @JimmyK4542 Link!). Same holds on elements of $S_2$ also, as both have same structure. This self reducing property on power is actually a good hint. It can shorten our methods

5. Path Score of a leaf node = Product of each Matrix Weight Value from leaf to the immediate child of the root of the tree(as root has no such value attached). Example Path Score of a leaf node, shown near to the arrow in the pic is given as

   Path Score of a leaf node(near to the arrow in pic)$=MWV_1(0)*MWV_1(1)*MWV_2(2)*MWV_1(4)$ . Remember multiplication order is very important as it is matrices

Question

1. What is the finte expression of the sum of all path-scores from all leaves(only) in-terms of n,for a given node index n.?

   2.NB :: You can even suggest separately for even and odd cases of n

   3.NB :: Even a partial solution is welcome,I can join in discussion

   4.NB :: We can find some similarity of the tree structure in huff man coding tree(in coloring) and Fibonacci tree. It may give more hints..

Thanks you for taking time to read it..

Answer 1

The desired sum of all (leaf) path scores can be regrouped, using the distributive law, into an expression matching the structure of the tree:       (I will write $V_1$ instead of $MWV_1$.)

$$ \left[\left[\left[\left[ V_1(0) \right] V_1(1) + V_2(0) \right] V_1(2) + \left[ V_1(0) \right] V_2(1) \right] V_1(3) + \left[\left[ V_1(0) \right] V_1(1) + V_2(0) \right] V_2(2) \right] V_1(4) + \left[\left[\left[ V_1(0) \right] V_1(1) + V_2(0) \right] V_1(2) + \left[ V_1(0) \right] V_2(1) \right] V_2(3) $$

This can be further simplified, since the number ("index") of a node uniquely determines the subtrees below it, so the same subexpressions appear over and over. This allows us to express these sums with a simple recurrence equation.

You defined the "path score" as going to the root of the tree. Let's define a "partial path score" as going only up to (and again not including) a certain node. Let $P(n)$ be the (matrix) sum of all partial path scores that only go up to a particular node with index $n$.

This gives us the efficient recursion $P(n) = \color{red}{P(n-1) \cdot \frac{1}{n} S_1} + \color{green}{P(n-2) \cdot \frac{1}{n} S_2}$, with $P(0)=1$ and $P(-1)=0$. After $n$ applications of this recursive formula, we get $P(n)$, which is the quantity desired in your question, for a tree with root index $n$.

Evaluating the recursion symbolically, we get: $$\begin{eqnarray} P(0) &=& 1 \\ P(1) &=& S_1 \\ P(2) &=& \frac{1}{2} (S_1^2 + S_2) \\ &=& \frac{1}{2} S_1^2 + \frac{1}{2} S_2 \\ P(3) &=& \frac{1}{3} ( \frac{1}{2} (S_1^2 + S_2) \cdot S_1 + S_1 S_2) \\ &=& \frac{1}{6} S_1^3 + \frac{1}{6} S_2 S_1 + \frac{1}{3} S_1 S_2 \\ P(4) &=& \frac{1}{4} ( \frac{1}{3} ( \frac{1}{2} (S_1^2 + S_2) \cdot S_1 + S_1 S_2) \cdot S_1 + \frac{1}{2} (S_1^2 + S_2) \cdot S_2) \\ &=& \frac{1}{24} S_1^4 + \frac{1}{24} S_2 S_1^2 + \frac{1}{12} S_1 S_2 S_1 + \frac{1}{8} S_1^2 S_2 + \frac{1}{8} S_2^2 \\ etc. \end{eqnarray}$$

These make a nice pattern, but it does not look like there will be a closed-form solution for the general case, especially since most terms do not involve high powers of $S_1$ or $S_2$, making it hard to take advantage of their skew symmetry.

For evaluation, the recursion (taking time linear in $n$) is much more efficient than these matrix polynomial forms (which have exponentially many terms).