0

Show that the cones $$ayz+bxz+cxy=0 \quad \text{and} \quad (ax)^\frac{1}{2}+(by)^\frac{1}{2}+(cz)^\frac{1}{2}=0$$ are reciprocal, the formar contains the co-ordinate axes while the latter touch the coordinte planes.

user326159
  • 3,277
Saroj Ghosh
  • 353
  • 1
    Two questions 1) What is your definition of "reciprocal" ? 2) There is a problem with the second equation: $ (ax)^\frac{1}{2}+(by)^\frac{1}{2}+(cz)^\frac{1}{2}=0$ represents the "equation" of point $(0,0,0)$... with the usual meaning of power 1/2 (i.e. with $(...)^{1/2} \geq 0$). If you use a different meaning, you must explain it. – Jean Marie Feb 19 '17 at 09:36
  • @JeanMarie we found out what reciprocal cones meant, http://math.stackexchange.com/questions/1714136/condition-for-cones-to-be-reciprocal/1714646#1714646 and http://math.stackexchange.com/questions/1899004/reciprocal-cone – Will Jagy Feb 19 '17 at 18:16
  • @Will Jagy Thanks for the definition. – Jean Marie Feb 20 '17 at 21:35
  • @JeanMarie I don't think the OP is capable of answering your question. Reading the handwritten page he posted as an answer gives one possible interpretation that makes sense. I posted one of the three reasonable orderings as a new answer. – Will Jagy Feb 20 '17 at 22:48

3 Answers3

2

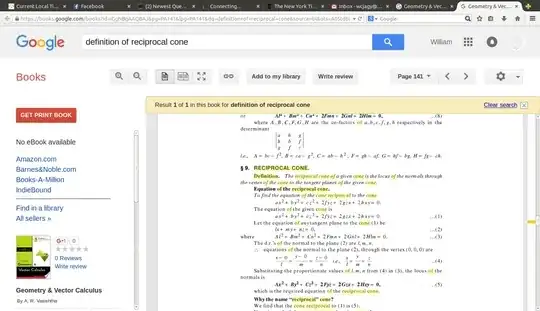
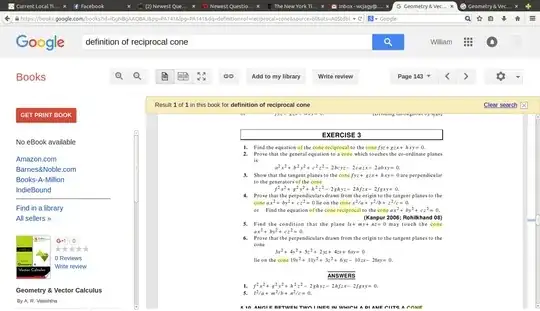
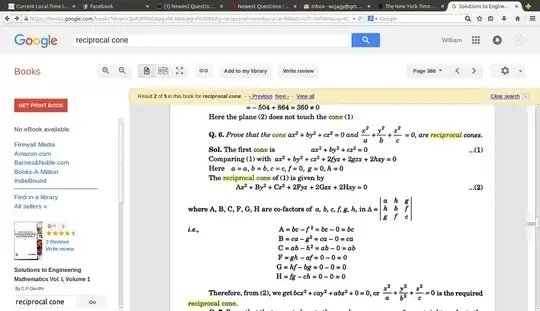
At some point I found the definition of reciprocal cone in this book. I posted some relevant pages at condition for cones to be reciprocal Alright, I was able to paste the same images here. Good to know how to do that, as I cannot seem to find those pages any more in the online book previews.

given cone $ayz + bzx + c xy = 0,$ the actual reciprocal cone is $$ a^2 x^2 + b^2 y^2 + c^2 z^2 - 2bcyz - 2cazx - 2abxy = 0. $$

About the coordinate planes, what happens when $z =0?$ Then $$ a^2 x^2- 2abxy + b^2 y^2 = (ax-by)^2 = 0, $$ so that $$ ax = by. $$ This is a single line, therefore the cone is tangent to the plane $z=0.$ Another way to confirm tangency is to point out that a point on this line is, for some $t,$ given by $(bt, at, 0).$ Furthermore, for a quadratic form given by $v^t H v,$ the gradient is given ( as a column vector) by $2 H v.$ We then calculate $$ \left( \begin{array}{rrr} a^2 & -ab & -ca \\ -ab & b^2 & -bc \\ -ca & -bc & c^2 \end{array} \right) \left( \begin{array}{r} bt \\ at \\ 0 \end{array} \right) = \left( \begin{array}{r} 0 \\ 0 \\ -2abct \end{array} \right) $$

$$ \left( \begin{array}{rrr} 0& c & b \\ c & 0 & a \\ b & a & 0 \end{array} \right) \left( \begin{array}{rrr} a^2 & -ab & -ca \\ -ab & b^2 & -bc \\ -ca & -bc & c^2 \end{array} \right) = \left( \begin{array}{rrr} -2abc & 0 & 0 \\ 0 & -2abc & 0 \\ 0 & 0 & -2abc \end{array} \right) $$

enter image description here

enter image description here

enter image description here

This seems to be a pretty good practice/solutions manual for this material

Community
  • 1
Will Jagy
  • 146,052
0

enter image description here.I able to 1st part but i can not understand 2nd part.

Saroj Ghosh
  • 353
  • 1
    I cannot understand the part about $\sqrt a x$ either. Were did you find this??? I don't see any way that describes a cone. – Will Jagy Feb 20 '17 at 04:24
  • 1
    @Will jagy, sorry somthing wrong in the last line , correct is (ax)^1/2+(by)1/2+(cz)^1/2=0 – Saroj Ghosh Feb 20 '17 at 05:52
  • 1
    Because this is not cone, paraboloid.　They are similar shape, though. – Takahiro Waki Feb 20 '17 at 08:19
  • With real constants $a,b,c, $ the equation $$ \sqrt {ax} + \sqrt {by} + \sqrt {cz} = 0 $$ refers to the single point (with real variables) $$ x = y = z = 0. $$ – Will Jagy Feb 20 '17 at 18:35
0

Alright, it turns out this was just carelessness about square roots. IF $$ \color{blue}{ax \geq 0, \; b y \geq 0, \; cz \geq 0 }$$ AND $$ \color{blue}{ \sqrt {cz} = \sqrt {ax} + \sqrt {by}}, $$ square once to get $$ cz = ax + by + 2 \sqrt {abxy}, $$ so $$ - ax - by + cz = 2 \sqrt {abxy}. $$ Squaring again does give $$ a^2 x^2 + b^2 y^2 + c^2 z^2 - 2byz -2ca zx + 2abxy = 2abxy, $$ $$ a^2 x^2 + b^2 y^2 + c^2 z^2 - 2byz -2ca zx - 2abxy = 0. $$ This is a subset of the cone in just one octant, and is not the entirety of cone points in that octant. We get three pieces when $$ \color{blue}{ax \geq 0, \; b y \geq 0, \; cz \geq 0 },$$ namely $$ \color{blue}{ \sqrt {cz} = \sqrt {ax} + \sqrt {by}}, $$ $$ \color{blue}{ \sqrt {ax} = \sqrt {by} + \sqrt {cz} }, $$ $$ \color{blue}{ \sqrt {by} = \sqrt {cz} + \sqrt {ax} }. $$

There is no sense to taking all $+$ signs, as in $$ \sqrt {ax} + \sqrt {by} + \sqrt {cz} = 0, $$ this can only be a single point!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

The example $a=b=c=1,$ with $x,y,z \geq 0,$ and $\sqrt z = \sqrt x + \sqrt y$ gives the satisfactory $$ z = x + y + 2 \sqrt {x y}. $$ This is part of a cone. We can write it in polar/cylindrical coordinates as $0 \leq \theta \leq \frac{\pi}{2},$ $$ z = r \; \left( \cos \theta + \sin \theta + 2 \sqrt { \cos \theta \; \sin \theta} \right) $$ Other points of the same cone in the first octant $x,y,z \geq 0,$ include $\sqrt x = \sqrt y + \sqrt z$ and $\sqrt y = \sqrt z + \sqrt x.$

Will Jagy
  • 146,052