(we will assume thereafter that $a,b,c$ are all nonzero).
There is no need to consider the reciprocal cone for this issue.
In fact, the general equation of such a cone is obtained by taking the product of the 4 expressions given to you :
$$\underbrace{(\sqrt{ax}+\sqrt{by}+\sqrt{cz})}_{f_0(x,y,z)}\underbrace{\color{red}{(\sqrt{ax}-\sqrt{by}+\sqrt{cz})}}_{f_1(x,y,z)}\underbrace{\color{green}{(\sqrt{ax}+\sqrt{by}-\sqrt{cz})}}_{f_2(x,y,z)}\underbrace{\color{blue}{(\sqrt{ax}-\sqrt{by}-\sqrt{cz})}}_{f_3(x,y,z)}=0\tag{1}$$
giving
$$f(x,y,z)=a^{2} x^{2} + b^{2} y^{2} + c^{2} z^{2} - 2 \, a b x y - 2 \, a c x z - 2 \, b c y z=0 \tag{2}$$
In this way, the locus of points verifying $f(x,y,z)=0$ is the union of the locii of points verifying $f_k(x,y,z)=0, k=0,1,2,3.$
The three parts of the cone defined by the three equations $f_k(x,y,z)=0, k=0,1,2,3$ have a nice pictorial representation as one can see on the figure below with the corresponding colors red, green blue (a half of the cone only has been represented for the sake of simplicity). Please note that equation $f_0(x,y,z)=0$ doesn't play any role because it is verified by a single point, the apex of the cone $(x,y,z)=(0,0,0)\cdots$
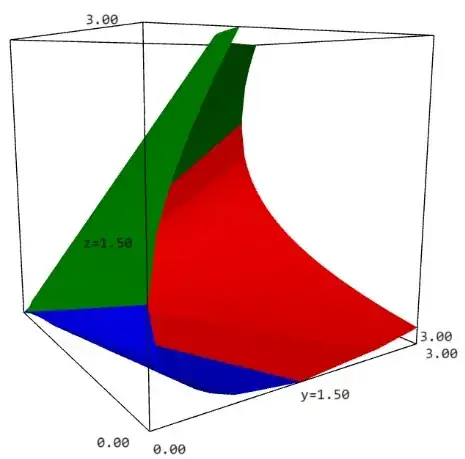
The 3 different "generating" lines (separating the different colored regions), have the following resp. equations:
$$D_x: \ \ \begin{cases}cz&=&by\\x&=&0\end{cases} \ \ D_y: \ \ \begin{cases}cz&=&ax\\y&=&0\end{cases} \ \ D_z: \ \ \begin{cases}by&=&ax\\z&=&0\end{cases}$$
Let us check for example that $D_x$ is tangent to coordinate plane $x=0$ is tangent to the cone along $D_x$ :
The generic equation of the tangent plane in point $(x_0,y_0,z_0)$ is
$$a^{2} xx_0 + b^{2} yy_0 + c^{2} zz_0- \, a b (x y_0+x_0y) - \, a c (x z_0+x_0z) - \, b c (y z_0+y_0z)=0 \tag{3}$$
Setting for example $(x_0,y_0,z_0)=(0,c,b)$ (one of the points of $D_x$) in (3), we get the equation of coordinate plane $x=0$, as awaited.
Edit : it is interesting to note that one can "logicaly" proceed from (2) to (1) by first writing (2) in the following form :
$$(ax-by-cz)^2=4bcyz$$
from which :
$$ax-by-cz=\pm 2 \sqrt{by}\sqrt{cz}$$
$$(\sqrt{ax})^2=(\sqrt{by})^2+(\sqrt{cz})^2\pm 2 \sqrt{by}\sqrt{cz}$$
$$(\sqrt{ax})^2=\left(\sqrt{by}\pm\sqrt{cz}\right)^2$$
$$\sqrt{ax}=\mp\left(\sqrt{by}\pm\sqrt{cz}\right)$$
giving the different factors of (1).
