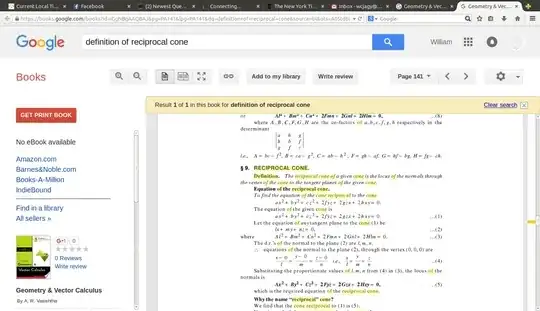
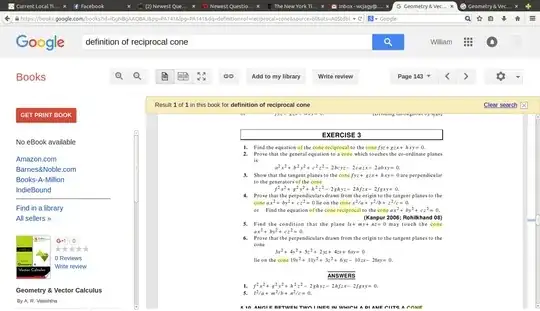
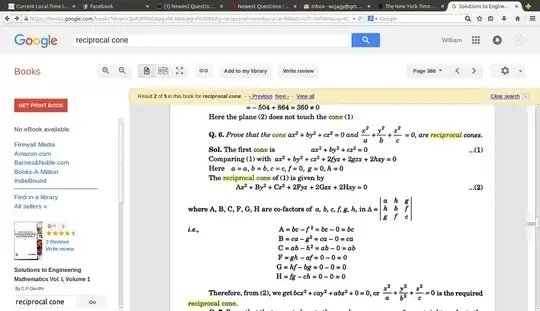
Question : Show that the cone $$ax^2 + by^2 + cz^2 - cxy - ayz - bzx = 0$$ is the reciprocal of the cone $$(a^2 - bc)x^2 + (b^2 - ac)y^2 + (c^2 - ab)z^2 - 2(a^2 + bc)yz - 2(b^2 + ac)zx - 2(c^2 + ab)xy =0$$
To me it seems like the that they can be proved using determinants but my instructor didn't covered this portion of the syllabus. Also my books didn't have any such thing or even minutely releated concept.
I was going through the previous year question papers and I saw this question. Kindly give me a hint to solve this. Is there any hint how to show this using determinant. I want to learn how to solve this.