1

Given some system $U*x = b$, I've solved for $x^*$, the least squares solution. I then compute the minimum squared error by $||U*x^* - b||^2$. I know that the least squares solution minimizes the sum of the squares of the errors made in the results of each equation, i.e. an approximate solution to the overdetermined system (in this case, U is 5x3). What is the significance of the minimum squared error as determined above? What does it tell me?

user2049004
  • 809

2 Answers2

0

A minimum mean-square error solution looks to minimize the average error in each element of the vector. So if the MSE is $\epsilon$, we can loosely say that each element of the vector has an error $\frac{\epsilon}{N}$.

Least squares is popular because of the nice closed form solution that it gives, not requiring any iterative algorithms to reach the answer.

Karthik Upadhya
  • 764
  • 7
  • 15
0

Given a matrix $\mathbf{U}\in\mathbb{C}^{m\times n}_{\rho}$, and a suitable data vector $b\in\mathbb{C}^{n}$, the linear system $$ \mathbf{U}x = b. $$ has a least squares solution defined by $$ x_{LS} = \left\{ x\in\mathbb{C}^{n} \colon \big\lVert \mathbf{U}x - b \big\rVert_{2}^{2} \text{ is minimized} \right\} $$

Define the residual error vector as $$ r = \mathbf{U}x - b, $$ the quantity which is minimized is the total error $$ r^{2} = \big\lVert \mathbf{U}x - b \big\rVert_{2}^{2} $$

b

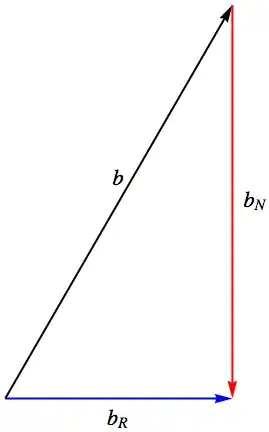
The figure above shows the data vector $b$. The blue vector is the projection of the data onto the range space $\color{blue}{\mathcal{R}\left( \mathbf{U}\right)}$. This piece is $$ \color{blue}{x_{LS}} = \color{blue}{\mathbf{U}^{+}b} $$

The residual error vector is the component of the data vector which passes through the null space $\color{red}{\mathcal{N}\left(\mathbf{U}^{*}\right)}$: $$ \color{red}{r} = \mathbf{U}\color{blue}{x_{LS}} - b = \color{blue}{b_{\mathcal{R}}} - b = \color{red}{b_{\mathcal{N}}} $$

The total error describes the magnitude of the component of the data vector which resides in the null space $$ \boxed{ r^{2} = \big\lVert \color{blue}{b_{\mathcal{R}}} - b \big\rVert_{2}^{2} = \big\lVert \color{red}{b_{\mathcal{N}}} \big\rVert_{2}^{2} } $$

Another example of interest: Finding the null space of a matrix by least squares optimization?

dantopa
  • 10,768