After some experimentation it seems that $\bf M v_0$ estimates the largest eigenvector. My intuition tells me that the relation between $\bf r$ and this eigenvector should affect the quality of this estimate, but I can't really figure out the relationship. Maybe scalar products are a good start.
The experiment setup:
$${\bf M}\in \mathbb R^{3\times 3}, \hspace{0.5cm}{\bf M}_{ij} = \mathcal N (\mu=0,\sigma=1) + 10\cdot {\bf vv}^T, \hspace{0.5cm}{\bf v} \in \mathbb R^{3\times 1}, {\bf v}_i = \mathcal N(\mu,\sigma=1)$$
After this ${\bf v}$ is normed to have $L_2$ norm 1.
Now doing: $${\bf v_0} = ({\bf M}^T{\bf M} + 10^3{\bf I})^{-1}(-2{\bf M}^T{\bf r} )$$
And then calculating the absolute value of the normed scalar product:
$$\frac 1 {\|{\bf Mv_0}\|} \cdot |<{\bf Mv_0}, {\bf v}>|$$ and stuffing into a histogram for 1024 different randomized $\bf r$:

In addition we have 2 straight-forward continuations
- Iterate the procedure for the found $\bf v_0$ to try and refine the estimate from last iteration.
- Solve for once for several $\bf v_0$ in parallel and then fuse the estimates.
The 2 is most straight forward to implement as we can expand column vectors $\bf v,r$ to matrices $\bf V,R$ where each column is a candidate eigendirection. Therefore we try it, also we choose to weight the candidate $\bf MV_0$ together using remappings of scalar products with $\bf R$ : $\text{diag}({\bf R}^T{\bf MV_0})^{\circ p}$ with $\circ p$ denoting Schur/Hadamard (elementwise) power function - and of course we must divide by the total sum. We leave out some practical details as for example make the internal scalar products positive so they don't give destructive interference in the weighted averaging. Let us call the averaged solution ${\bf V_{0s}}$.
Then what remains to find a complete eigensystem is to update the above system to forbid the previously found eigenvectors. Our approach here is to successively update the left hand side $\bf L$ and right hand side $\bf r$ by adding $${\bf L} \stackrel{+}{=} \epsilon {\bf V_{0s}}{\bf V_{0s}}^T\\{\bf r} \stackrel{+}{=} {{\bf M}^T \bf V_{0s}}$$
This will of course only be theoretically acceptable if we expect an orthogonal system of eigenvectors, but it's a start!
A typical "lucky" scalar product matrix we could get with 8 fused candidate directions for each eigenvector ( perfect would be $100 \cdot {\bf I}_3$ ):
$$100\cdot {\bf S_0}^T{\bf S} \approx \left[\begin{array}{ccc}
100&-13&-1\\-4&100&1\\0&0&100\end{array}\right]$$
( $\bf S$ is the "true" matrix in ${\bf M} = {\bf SDS}^{-1}$ given by computer-language builtin "eig" command and $\bf S_0$ is the estimate given by our method. )
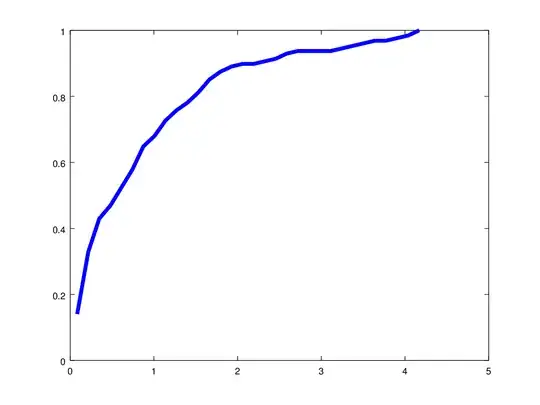
An accumulated error histogram (cumulative distribution function) using the error $\|{\bf S_0}^T{\bf S - I}_3\|_1$ (for our example above it is $\frac{13+1+4+1}{100} = 0.19$):