5

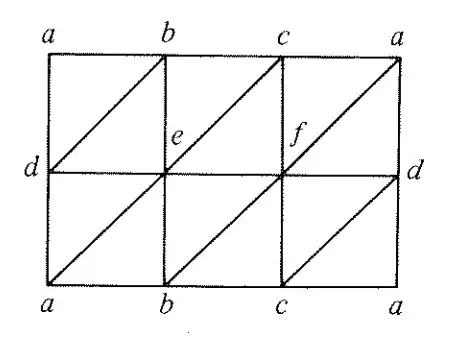
I refer to example 4, fig.3.6, p.17 of Munkres' Algebraic Topology. He says the given triangulation scheme "does more than paste opposite edges together".

Not clear to me. For those who don't have the book to hand, a rectangle is divided into 6 equal squares by a horizontal midline and two verticals; each square has a south-west to north-east diagonal.

enter image description here

Watson
  • 24,404
InTransit
  • 646
  • 3
    Any chance you could add the picture? – Michael Albanese Jun 05 '14 at 07:10
  • 6
    I believe the issue is that if a simplex has vertices ${v_0, ..., v_n}$, then that collection of vertices should uniquely identify that $n$-simplex. In the case of the surface, subdivided as you have described, this fails. For example, if you take a vertex on the "midline" and the vertex directly above it (which is the same as the one below it by gluing), those two vertices should belong to a unique segment. But, they don't. – Sammy Black Jun 05 '14 at 07:21
  • @MichaelAlbanese Got to figure out how to do it. But it's really a standard sort of triangulation diagram. – InTransit Jun 06 '14 at 15:21
  • @SammyBlack Thanks, I'll see if this sort of argument works on other non-triangulations. – InTransit Jun 06 '14 at 15:24
  • 2
    http://math.stackexchange.com/questions/686142/a-diagram-which-is-not-the-torus – user135520 Jan 11 '15 at 19:08

2 Answers2

8

Better late than never. The definition of a simplicial complex reads as follows.

A finite (Euclidean) simplicial complex is a finite collection $K$ of simplices in some Euclidean space $\mathbb{R}^n$, satisfying the following two conditions:

  • If $\sigma \in K$, then every face of $\sigma$ is in $K$.
  • The intersection of any two simplices in $K$ is either empty or a face of each.

Now in this case the second point is violated. Consider the triangles $bef$ and $ebc$, then their intersection is $\{e,b\}$ which is not a face of each.

TheGeekGreek
  • 8,158
1

Paste the top and bottom edges first to get a cylinder. Look at the circle on one end. One half of the circle is identified with the other half as each is da. So collapse that circle down to a line. Now do the same at the other end. Looks like a toothpaste tube with two bottoms and no top. Now identify the two ad ends. You get a torus with one circle circle on it collapsed to a segment. Looks like this: https://mathcurve.com/surfaces.gb/klein/toredeklein.shtml

Eugene Curtin
  • 11