The following is taken from Munkres' Algebraic Topology book.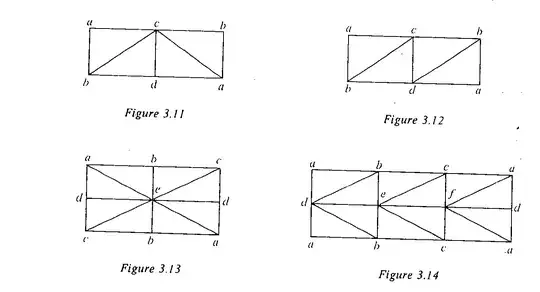
I tried to determine which spaces (e.g. Mobius Strip, Klein bottle, etc) these complexes are, but to no avail.
I computed the Euler Characteristics (V-E+F) to be -1, -1, 1, -1 respectively. (top left, top right, bottom left, bottom right). However, I don't know any spaces with $\chi=-1$. The one with $\chi =1$ could be either a disk or a projective plane.
I am guessing that they may be trick questions (i.e. not valid triangulations). CW complexes are not discussed yet in the book, hence this rules out CW complexes or cell complexes.
Thanks for any help!