Determining if an arbitrary point lies inside a triangle defined by three points?

Question

Is there an algorithm available to determine if a point P lies inside a triangle ABC defined as three points A, B, and C? (The three line segments of the triangle can be determined as well as the centroid if they are needed.)

Grid space is defined as Screen Space, that is, 2D Cartesian with the Y-Axis flipped so "up" is negative y and the origin is the upper left corner.

Answer 1

This is a fairly well known algorithm. It all comes down to using the cross product. Define the vectors $AB$, $BC$ and $CA$ and the vectors $AP$, $BP$ and $CP$. Then $P$ is inside the triangle formed by $A, B$ and $C$ if and only if all of the cross products $AB\times AP$, $BC\times BP$ and $CA\times CP$ point in the same direction relative to the plane. That is, either all of them point out of the plane, or all of them point into the plane.

Update: this test can be performed using dot products.

Update 2: As emphasised in the comments, you only have to compare signs of the third components.

Answer 2

Method

To test any point $P=(x,y)$, first move the origin at one vertex, like $A$ such that $$ B \rightarrow B - A $$ $$ C \rightarrow C - A $$ $$ P \rightarrow P - A $$

Then I calculate the scalar $ d = x_B y_C - x_C y_B $ and the three Barycentric weights

$$ \begin{matrix} w_A = \frac{ x ( y_B-y_C) + y ( x_C-x_B) + x_B\; y_C - x_C\; y_B}{d} \\ w_B = \frac{ x\; y_C - y\; x_C }{d} \\ w_C = \frac{ y\; x_B - x\; y_B }{d} \end{matrix} $$

The point is inside when all weights are between $0\ldots1$.

Examples

Example: $A=(1,1)$ $B=(4,2)$ $C=(2,7)$. Consider a point $P=(2,3)$ then the scalar is: $d=17$ and three weights are: $w_A = \frac{8}{17}$, $w_B = \frac{4}{17}$ and: $ w_C=\frac{5}{17}$ which are all $w_i \geq 0$ and $w_i \leq 1$.

On the other hand if $P=(1.5,5)$ then: $w_A = \frac{13}{34} $, $w_B = -\frac{1}{17}$ and: $ w_C=\frac{23}{34}$ and since $w_B$ does not fall between $0\ldots1$ then the point is outside.

Proof

Use homogeneous coordinates with: $A=(x_A,y_A,1)$, $B=(x_B,y_B,1)$, $C=(x_C,y_C,1)$, $P=(x,y,1)$ and use the following relation $$ P = w_A\;A + w_B\;B+w_C\;C $$ to solve for $w_A$, $w_B$ and $w_C$.

The notice that the equation $w_A=0$ described the line $BC$ and the equation $w_A=1$ a line parallel to $BC$ through $A$. Similarly for the other weights. The region where all the weights are $w_i\geq0$ and $ w_i\leq1$ is the triangle described by $ABC$.

Appendix

The more general procedure uses vector cross products to get the weights, without having to shift the origin to $A$. Given the original 2D or 3D vectors $A$, $B$, $C$ and $P$ the barycentric weights are

$$ \begin{aligned} w_A & = \tfrac{ B \times C + P \times (B-C) }{ A\times B + B \times C + C \times A } \\ w_B & = \tfrac{ C \times A + P \times (C-A) }{ A\times B + B \times C + C \times A } \\ w_C & = \tfrac{ A \times B + P \times (A-B) }{ A\times B + B \times C + C \times A } \\ \end{aligned} $$

where $A \times B = x_A \, y_B - y_A \, x_B$ for 2D vectors, and similarly for the rest of the cross products.

C# Code

The code below is tested and it works

public bool GetWeights(Vector2 point, out double w_A, out double w_B, out double w_C)
{
    double xd = Cross(A, B) + Cross(B, C) + Cross(C, A);

    if (Abs(xd) > 1e-13)
    {
        double xa = Cross(B, C) + Cross(point, B - C);
        double xb = Cross(C, A) + Cross(point, C - A);
        double xc = Cross(A, B) + Cross(point, A - B);

        w_A = xa / xd;
        w_B = xb / xd;
        w_C = xc / xd;
    }
    w_A = 0;
    w_B = 0;
    w_C = 0;
    return false;
}

public static double Cross(Vector2 a, Vector2 b) => a.X*b.Y - a.Y*b.X;

Answer 3

Given three non-collinear points in $\mathbb{R}^2$ (the vertices of a triangle) $A,B,C$ and a point $P$, there is a unique way to represent $P$ as $$ P=\lambda_A A + \lambda_B B + \lambda_C C $$ with $\lambda_A,\lambda_B,\lambda_C$ being real coefficients fulfilling $\lambda_A+\lambda_B+\lambda_C=1$. This kind of representation is also known as exact barycentric coordinates. The coefficients $\lambda_A,\lambda_B,\lambda_C$ are straightforward to find through linear algebra and the point $P$ strictly lies on the interior of $ABC$ iff $$\lambda_A>0,\quad\lambda_B>0,\quad\lambda_C>0,$$ that is equivalent to $$ \begin{pmatrix}1 & 1 & 1 \\ x_A & x_B & x_C \\ y_A & y_B & y_C\end{pmatrix}^{-1} \begin{pmatrix}1 \\ x_P \\ y_P\end{pmatrix}>0. $$

An equivalent alternative, assuming that $A,B,C$ are counter-clockwise ordered, is to compute the (oriented) areas of $ABP,BCP,CAP$ through the shoelace formula and check that all these (oriented) areas are positive.

Update. The (seemingly) most efficient approach just requires $\color{red}{6}$ multiplications (as already studied on SO). Without loss of generality, by using a translation we may assume that $A$ is the origin. Up to relabeling $B$ and $C$, we may also assume that $O,B,C$ are counter-clockwise oriented. Let $\varphi$ be the linear map bringing $B$ to $(1,0)$ and $C$ to $(0,1)$: $P$ lies inside $OBC$ iff $\varphi^{-1}(P)$ lies inside the right isosceles triangle with vertices at $(0,0),(1,0),(0,1)$, so in order to check if $P$ lies inside $OBC$ we just have to set $$ v = \begin{pmatrix}y_C & -x_C \\ -y_B & x_B \end{pmatrix}\begin{pmatrix}x_P \\ y_P\end{pmatrix},\qquad D=x_B y_C-x_C y_B $$ then check that all the conditions $$ v_x > 0,\qquad v_y > 0,\qquad v_x+v_y < D $$ hold. Just $\color{red}{6}$ multiplications and a few comparisons/sums/subtractions are involved.

Answer 4

I think you could check by computing the area of $\triangle ABC$, $\triangle ABP$, $\triangle BCP$, and $\triangle ACP$ (which can be done relatively easily from the coordinates of the points), and if $k_{\triangle ABC}=k_{\triangle ABP}+k_{\triangle BCP}+k_{\triangle ACP}$ (where $k_\_$ is the area), then $P$ is inside the triangle (or possibly on its boundary), but if $k_{\triangle ABC}< k_{\triangle ABP}+k_{\triangle BCP}+k_{\triangle ACP}$, $P$ is outside the triangle.

Answer 5

Yes, this problem certainly has come up a lot before. Eric Haines wrote about the more general "point in polygon" problem (whose algorithms can be vastly simplified for the triangular case) in Graphics Gems IV. He also presented a method using barycentric coordinates in this Dr. Dobb's Journal article.

Answer 6

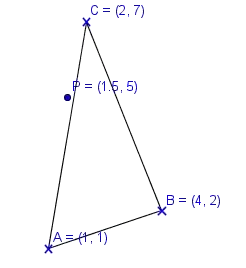
I just thought I would add an example of one implementation of the algorithm that the accepted answer recommends. It only does the absolutely necessary bits, and fails quickly. (JavaScript)

Thanks to https://stackoverflow.com/a/9755252/5946596. This is essentially that code with explanations. I did not understand what it was doing when I first looked at it, but writing the code to do the full accepted answer algorithm snapped it into place.

Start the function. a, b, c implement {x:number, y:number} and are the vertices of the triangle A, B, C. point is P, the point being checked.

function triangleContains(point, a, b, c) {

Get the vector between A and the point P.

const AP = {x:point.x - a.x, y:point.y - a.y}

(b.x - a.x), (b.y - a.y) is side AB, and is "clockwise". We'll do just the third term of the crossproduct ABxAP, and then only keep its direction.

const AB = {x:(b.x - a.x), y:(b.y - a.y)}
const thirdTermABxAPisPositive = AB.x  * AP.y - AB.y * AP.x > 0;

(c.x - a.x), (c.y - a.y) is side AC, and is "counter clockwise" from AB. Again we'll do just the third term of the crossproduct ACxAP, caring only about its direction. By using the "counter clockwise" AC instead of CA we have saved having to calculate CP.

const AC = {x:(c.x - a.x), y:(c.y - a.y)}
const thirdTermACxAPisPositive = AC.x * AP.y - AC.y * AP.x > 0

This result should NOT match the direction of what we kept before because AC and AB are in different directions. We can go ahead and exit the function returning false.

if (thirdTermACxAPisPositive == thirdTermABxAPisPositive) return false;

(c.x - b.x), (c.y - b.y) is sideBC and like the first side is "clockwise". (point.x - b.x),(point.y - b.y) is the vector BP. One last time, we only care about the third term of the crossproduct BCxBP, and really just its direction.

const BC = {x:(c.x - b.x), y:(c.y - b.y)}
const BP = {x:(point.x - b.x), y:(point.y - b.y)}
const thirdTermBCxBPisPositive = BC.x * BP.y - BC.y * BP.x > 0

This value should match the direction of thirdTermABxAPisPositve because BC is the same direction as AB. If it doesn't, again we can go ahead and leave the function, returning false.

if (thirdTermBCxBPisPositive != thirdTermABxAPisPositive) return false;

If we made it this far, then we're inside because all the booleans have the same value. It does not matter if they are all true or all false, they just have to be all the same.

return true; }

All together

function triangleContainsE(point, a, b, c) {
const AP = {x:point.x - a.x, y:point.y - a.y}

const AB = {x:(b.x - a.x), y:(b.y - a.y)}
const thirdTermABxAPisPositive = AB.x  * AP.y - AB.y * AP.x > 0;

const AC = {x:(c.x - a.x), y:(c.y - a.y)}
const thirdTermACxAPisPositive = AC.x * AP.y - AC.y * AP.x > 0

if (thirdTermACxAPisPositive == thirdTermABxAPisPositive) return false;

const BC = {x:(c.x - b.x), y:(c.y - b.y)}
const BP = {x:(point.x - b.x), y:(point.y - b.y)}
const thirdTermBCxBPisPositive = BC.x * BP.y - BC.y * BP.x > 0

if (thirdTermBCxBPisPositive != thirdTermABxAPisPositive) return false;

return true; 


}

Not Mixing Directions Example, recommend in comment by orig. author

function triangleContains_NotMixingDirections(point, a, b, c) {
const AP = { x: point.x - a.x, y: point.y - a.y };
const AB = { x: (b.x - a.x), y: (b.y - a.y) };
const thirdTermABxAPisPositive = AB.x * AP.y - AB.y * AP.x > 0;

const BC = { x: (c.x - b.x), y: (c.y - b.y) };
const BP = { x: (point.x - b.x), y: (point.y - b.y) };
const thirdTermBCxBPisPositive = BC.x * BP.y - BC.y * BP.x > 0;

if (thirdTermBCxBPisPositive != thirdTermABxAPisPositive)
    return false;

const CA = { x: (a.x - c.x), y: (a.y - c.y) };
const CP = { x: (point.x - c.x), y: (point.y - c.y) };
const thirdTermCAxCPisPositive = CA.x * CP.y - CA.y * CP.x > 0;

return (thirdTermCAxCPisPositive == thirdTermABxAPisPositive);

}

Answer 7

Let us suppose point $P$ is inside $\triangle ABC$. Consider the line passing through $A$ and $B$. It divides the plane into two zones. $P$ and $C$ are in the same zone (why?). This simple property allows us to write an algorithm that answers OP's question.

Pick any vertex, see if that vertex and $P$ are on the same side of the line passing through the other two vertices. If the answer is yes for any selected vertex, then $P$ is inside $\triangle ABC$.

This method can be generalized for convex polygons, if the order of the vertices is given.

Note: to check if two points are on the same side of the line, plug the coordinates of each point in the equation of the line. The two points are on the same side of the line if and only if the two calculated numbers have the same sign.

Answer 8

I wrote a complete article about point in triangle test. It shows the barycentric, parametric and dot product based methods.

Then it deals with the accuracy problem occuring when a point lies exactly on one edge (with examples). Finally it exposes a complete new method based on point to edge distance.

http://totologic.blogspot.fr/2014/01/accurate-point-in-triangle-test.html

Enjoy !

Answer 9

Here's a vector-based approach.

The theory

Consider the following $\triangle ABC$ and two vectors $\vec{a} := \vec{AB}, \vec{b} := \vec{AC}$.

Because $ABC$ is a triangle, $\{\vec{a}, \vec{b}\}$ is a basis of $\mathbb{R}^2$. Let $P$ be any point on the plane. Let $\vec{p} := \vec{AP}$. Then, there exists unique $x,y$ such that $\vec{p} = x\vec{a} + y\vec{b}$.

I claim that $P$ is in $\triangle ABC$ if and only if $$ \begin{equation} \begin{aligned} &0 \le x,y \le 1 \quad \hbox{and}\\ &0 \le x+y \le 1 \end{aligned} \tag{1} \end{equation} $$

Suppose that $P$ is in $\triangle ABC$. Now we connect $AP$ and extend it until it intersects $BC$ at $D$. We have $\vec{AD} = \vec{a} + t\vec{BC} = t\vec{b} + (1-t)\vec{a}$, where $0 \le t \le 1$. Then, we have, for $0 \le \lambda \le 1$, $$ \vec{AP} = \lambda\vec{AD} = \lambda t\vec{b} + \lambda(1-t)\vec{a} $$ So, $x = \lambda(1-t), y =\lambda t$, and they clearly satisfy (1).

Suppose that $P$ is not in $\triangle ABC$, then we have two situations.

1. (The ray $AP$ is within $\angle BAC$): If we extend $AD$ further to a $P'$ outside of the triangle, then we will have $\lambda > 1$, and thus $x+y > 1$.
2. (The ray $AP$ is not within $\angle BAC$): If we rotate $AP$ to go beyond $AB$ or $AC$, then we will have to have either $x$ or $y$ being negative (or both).

Now we have proven that:

1. If $P$ is in $\triangle ABC$, then (1) holds.
2. If $P$ is not in $\triangle ABC$, then (1) does not hold.

Because of the uniqueness of $x,y$, their converses hold. We have finished the proof. $\square$

The algorithm

$x,y$ can be found by solving the equation $\vec{AP} = x\vec{a} + y\vec{b}$, which involves a $2\times 2$ matrix, and there are plenty of fast algorithms to do that.

Alternatively, you can solve once for the formulae of $x$ and $y$, and hard-code them into your program:

Verifying if $x,y$ satisfy (1) is straightforward.