1

I want a definitive front-to-back triangle drawing order under orthographic projection.

This is an X-post due to inactivity on the other: https://tex.stackexchange.com/q/735053/319072

Note: I have tried to implement the algorithm that was suggested in the comments using Lua in https://stackoverflow.com/q/79625710/29000697, but I'm not having success.

First we project the triangles onto the plane through the origin which is orthogonal to the observer vector. If a point of one triangle is contained within the other, then we take the vector to the corresponding point on its non-projected counterpart from the plane through the other non-projected triangle.

If the dot product of this vector, and the a normal of the plane whose dot product with the observer vector is positive, is positive, then the triangle is in front of the one in the plane. otherwise, it is behind.

If there is no point on one projected triangle which is within the other, then we sort them by centroid.

I have a rectangle in the $uv$-Cartesian grid, on the domain $u\in[a,b]$ and $v\in[c,d]$. I sample the grid differently in both directions. For $u$, I take $u_{s}$ samples, and for $v$ I take $v_{s}$ samples. This breaks the plane into a bunch of adjacent rectangles - a "quasi-grid" so-to-speak. Then I triangulate this grid by connecting the lower left vertice to the upper right vertice for every rectangle.

This triangulation enables me to generate a triangulated parametric surface, given enough samples. [NOTE: For this question, we can assume that the surface does not intersect itself. We can also assume that there is no cyclic overlapping.] For example, $$ r(u,v) = \bigl(x(u,v),\,y(u,v),\,z(u,v)\bigr) $$ I need to draw these parametrically mapped triangles in an order so that, under orthographic projection onto the $xy$-plane, no triangle ever paints over one that should be in front.

Right now I simply sort these triangles by the dot product of their centroid with the vector that faces the observer. See How does the dot product give correct depth ordering in orthographic 3D projections?.

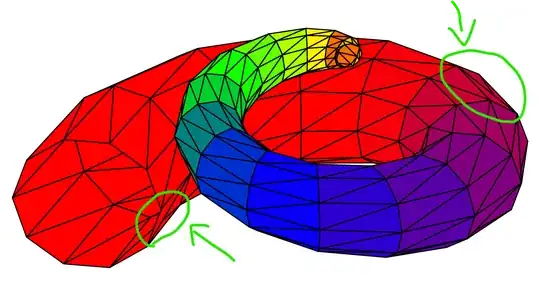
When the surface is not evenly distributed - for example, if one of the parameters grows at an increasing rate - the centroids of some triangle in the background can actually lie closer than parts of a triangle in the foreground, so the hind triangle is drawn in front.

My goal is to find a definitive Boolean litmus test to determine whether one triangle is in front of another or not with respect to an observer vector, using only the list of triangles with their vertex coordinates.

Aside from centroid sorting, I tried only drawing front facing triangles, but the problem still occurs with them.

What is a definitive test I can use to sort triangles in a 3D orthographic projection?

Here is a visual of the layering problem:

output

P123
  • 213
  • 10
  • I think doing an adjacency check with the signed distance from the tip of one to the plane through the other would work in this case, but I want something truly definitive – P123 May 10 '25 at 02:43
  • 1
    One fairly brute force way is: compute the intersection of the two triangles in XY plane; if it is empty, order triangles arbitrarily; otherwise, take any point inside the intersection (e.g. one of the vertices of the intersection) and order according to the Z coordinate of this point. – lisyarus May 10 '25 at 03:39
  • @lisyarus By XY plane, do you mean the plane which is orthogonal to the viewing vector? If so, that sounds like it would work. Let me try and implement it. This is a non-trivial task, so I will need some time. Thank you for your time and help. By the way, how should I tell if a point on the plane is within a triangle on that same plane? I know how to get the coordinates in the plane's orthonormal basis already. Really good idea, by the way! – P123 May 10 '25 at 03:52
  • 1
    @lisyarus Oops, in the question it is definitely the xy plane, pardon my mis-correction in my previous comment. – P123 May 10 '25 at 03:57
  • https://math.stackexchange.com/a/51328/1499599 – P123 May 10 '25 at 04:03
  • 1
    What I would do is: for each edge of the first triangle, find the linear function ($ax+bx+c$ with $(a,b)$ being the edge's normal) which is zero on this edge, and which is positive inside the triangle (you'll need to figure out if the triangle is CW or CCW in XY plane). Then apply this function to the three vertices of the other triangle. You have three cases: 1) all vertices are outside => triangles don't intersect, 2) all vertices are inside => move to the next edge, 3) some vertices are inside, some outside => this edge might intersect two edges... – lisyarus May 10 '25 at 04:14
  • 1
    ...from the second triangle => compute the intersection points, check if they are on the edges (and not just on the lines containing the edges), use one of them as your witness for ordering. If this didn't give you the result, repeat the same process with the triangles swapped (iterate edges of the second triangle, test vertices of the first triangle). Either the triangles don't intersect, which will be found in case 1, or one is inside the other, which will be found in case 2, or they have intersecting edges, found in case 3. – lisyarus May 10 '25 at 04:14
  • 1
    @lisyarus I know an algorithm to make the points of a given triangle counter-clockwise to ease the process. Thank you very much for your help. This is a complex algorithm, so I will need maybe a day or two to set it up right with the new logic (especially since my current algorithm is written in TeX, and I'm converting it to Lua, which will take time). – P123 May 10 '25 at 04:38

1 Answers1

1

Perhaps you know BSP trees produces perfect front-to-back ordering of polygons ([2]). Classic BSP tree is a binary tree storing partition planes in the nodes and convex subspaces at the leaves. To build a BSP tree you pick a plane which splits the polygons in two groups of approx same size ans set as the root node, then classify each polygon as either behind or in front of the plane. Store the behind polygons in one branch, the in front in another (depending on polygon orientation). Then repeat the same operation on each branch recursively. The key point is that if a polygon cannot be classified as behind or in front the plane, that polygon must be splitted in two and each half is classified accordingly. This is the price to pay to use BSP trees, however I am not aware of other method to have perfect front-to-back ordering without using z-buffers.

BSP-tree works with orthographic projection ([1]).

[1] https://stackoverflow.com/questions/58685960/orthographic-projection-and-bsp-tree-to-render-objects-from-back-to-front

[2] https://people.eecs.berkeley.edu/~jrs/274/bsptreefaq.html

Mauricio Cele Lopez Belon
  • 1,653
  • Thank you very much for offering this solution. I will accept since it will work, though I am certain that there must be an algorithm which doesn't break apart triangles when the triangles don't intersect and don't overlap cyclically. – P123 May 18 '25 at 00:32
  • 1
    If all triangles form a mesh then maybe "topological order" can be used to aid spatial order and avoid triangle split. But that deserves research. – Mauricio Cele Lopez Belon May 18 '25 at 07:04