Find the inellipse of a triangle with its major axis pointing in a given direction and with a given ratio of major to minor

Question

In a recent post I've investigated the ellipse tangent to the $x$ and $y$ axes as well as a third given line.

In this problem, you're given a triangle with known vertices, and your task is to find the inscribed ellipse that is tangent to all three sides of the triangle. Since there is an infinite number of these ellipses, we have to narrow it down. So assume that you are also given the direction of the major axis as the angle it makes with the $+x$-axis direction, and also you're given the ratio of the major to minor axes.

This is the task: Finding the equation of the ellipse under the given conditions.

I appreciate your input, comments, hints, and solutions.

My attempt:

Assume the vertices of the triangle are the three points $\mathbf{p_1, p_2, p_3}$.

The equation of the ellipse to be found is

$ (\mathbf{r - C})^T Q (\mathbf{r - C}) = 1$

where $\mathbf{C}$ is the center of the ellipse.

From $ \mathbf{p_1, p_2, p_3}$ we can compute the normal vectors to the sides $\mathbf{p_1 p_2 , p_2 p_3 , p_3 p_1}$, let's call these $\mathbf{n_1, n_2, n_3} $ respectively.

Let the tangency points on these sides be $\mathbf{r_1, r_2, r_3}$ respectively.

Since the direction of the major axis is given as the angle $\theta$ it makes with $+x$ axis, then it has the form

$ Q = R D R^T $

where $ D = \begin{bmatrix} \dfrac{1}{a^2} && 0\\ 0 && \dfrac{1}{b^2} \end{bmatrix} $

And $ R = \begin{bmatrix} \cos \theta && - \sin \theta \\ \sin \theta && \cos \theta \end{bmatrix} $

Carrying out the multiplication, gives the following expression for $Q$:

$ Q = \begin{bmatrix} \dfrac{1}{a^2} \cos^2 \theta + \dfrac{1}{b^2} \sin^2 \theta && \sin \theta \cos \theta \left( \dfrac{1}{a^2} - \dfrac{1}{b^2} \right)\\ \sin \theta \cos \theta \left( \dfrac{1}{a^2} - \dfrac{1}{b^2} \right) && \dfrac{1}{a^2} \sin^2 \theta + \dfrac{1}{b^2} \cos^2 \theta \end{bmatrix} $

Now let the ratio of the major axis to the minor axis be $r$ then

$ a = r b $

Substituting this into the above equation gives

$ Q = \dfrac{1}{b^2} Q_0 $

where

$ Q_0 = \begin{bmatrix} \dfrac{1}{r^2} \cos^2 \theta + \sin^2 \theta && \sin \theta \cos \theta \left( \dfrac{1}{r^2} - 1 \right)\\ \sin \theta \cos \theta \left( \dfrac{1}{r^2} - 1 \right) && \dfrac{1}{r^2} \sin^2 \theta + \cos^2 \theta \end{bmatrix} $

Note that $Q_0$ is known.

Now the gradient vector at the tangency points $\mathbf{r_i}, i = 1,2,3 $ is given by

$ \mathbf{g_i} = 2 Q (\mathbf{r_i - C} ) $

And assuming the $\mathbf{n}_i $ are pointing outward from the triangle then we have

$ Q(\mathbf{r_i - C} ) = k_i \ \mathbf{n_i} $

From which

$ \mathbf{r_i - C} = k_i Q^{-1} \ \mathbf{n_i} $

Now let

$ P = Q^{-1} = b^2 Q_0^{-1} = b^2 P_0 $

Then

$ \mathbf{r_i - C} = k_i b^2 P_0 \mathbf{n}_i $

Substituting this into the equation of the ellipse, gives

$ k_i = \dfrac{1}{b \sqrt{ \mathbf{n}_i P_0 \mathbf{n}_i } }$

so that

$ \mathbf{r_i - C} = b \dfrac{ P_0 \mathbf{n_i}}{ \sqrt{ \mathbf{n}_i P_0 \mathbf{n}_i }} $

Pre-multiplying this with $\mathbf{n}_i^T $ gives

$ \mathbf{n_i}^T (\mathbf{r_i - C}) = b \sqrt{ \mathbf{n}_i P_0 \mathbf{n}_i } $

Now,

$\mathbf{n_i}^T (\mathbf{r_i - C}) = \mathbf{n_i}^T (\mathbf{r_i - p_i + p_i - C}) = \mathbf{n_i}^T (\mathbf{p_i - C} ) $, because $\mathbf{n_i}^T (\mathbf{r_i - p_i} ) = 0 $

Consequently, we now have the following equations

$ \mathbf{n_i}^T (\mathbf{p_i - C} ) = b \sqrt{ \mathbf{n}_i P_0 \mathbf{n}_i } , i = 1, 2, 3$

And this is a $3 \times 3$ linear system in the two coordinates of $\mathbf{C}$ and $b$ and can be readily solved.

This completes the specification of the ellipse.

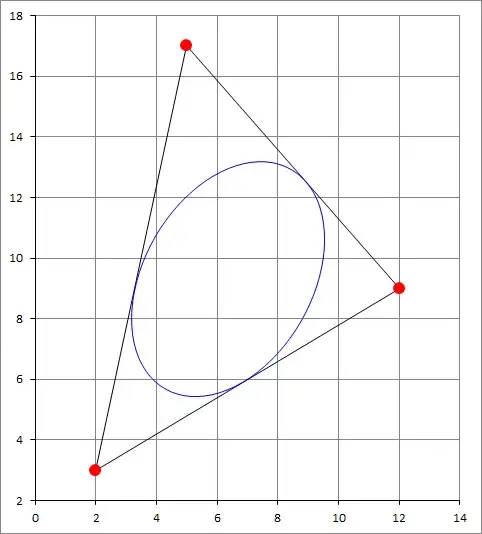
The image below depicts the inellipse generated for the triangle with vertices $\mathbf{p_1} = (2,3), \mathbf{p_2} = (12,9) , \mathbf{p_3} = (5,17) $ using the above formulas. The angle of the major axis is specified as $60^\circ$ and the ratio of major to minor is $1.5$.

Answer 1

Following the idea presented by @David K in his comment above, I will first transform the given triangle vertices by scaling by $r = \dfrac{b}{a}$ along the direction $V = (\cos \theta , \sin \theta) $. This scaling transformation is given by

$ S = R S_1 R^T $

where

$ R = \begin{bmatrix} \cos \theta && - \sin \theta \\ \sin \theta && \cos \theta \end{bmatrix} $

And

$ S_1 = \begin{bmatrix} r && 0 \\ 0 && 1 \end{bmatrix} $

So that

$ S = \begin{bmatrix} r \cos^2 \theta + \sin^2 \theta && \cos \theta \sin \theta (r - 1) \\ \cos \theta \sin \theta (r - 1) && r \sin^2 \theta + \cos^2 \theta \end{bmatrix} $

Now applying $S$ to the three vertices $\mathbf{p_1}, \mathbf{p_2}, \mathbf{p_3}$ we obtain their images $\mathbf{p'_1}, \mathbf{p'_2}, \mathbf{p'_3}$ respectively. The image of our desired ellipse becomes the incircle of $\triangle \mathbf{p'_1 p'_2 p'_3 } $. The radius of this incircle is

$ r_i = \dfrac{2 A}{P} $

where $A , P $ are the area and perimeter of $\triangle \mathbf{p'_1 p'_2 p'_3} $.

The incenter $\mathbf{C'_i}$ is given by

$ \mathbf{C'_i} = \dfrac{ \ell_1 }{P} \mathbf{p'_1} + \dfrac{ \ell_2}{P} \mathbf{p'_2} + \dfrac{\ell_3}{P} \mathbf{p'_3} $

where $\ell_1 = | \mathbf{p'_2 p'_3} | , \ell_2 = | \mathbf{p'_1 p'_3} | , \ell_3 = | \mathbf{p'_1 p'_2} | $

And now the equation of the incircle is

$ (\mathbf{r' - C'_i})^T (\mathbf{r' - C'_i}) = r_i^2 $

where $r' = [x', y']^T$. Since $r' = S r $, then the equation of our desired ellipse is

$ ( S \mathbf{r} - \mathbf{C'_i} )^T ( S \mathbf{r} - \mathbf{C'_i} ) = r_i^2 $

which re-arranges to

$ (\mathbf{r} - S^{-1} \mathbf{C'_i} )^T S^T S (\mathbf{r} - S^{-1} \mathbf{C'_i} ) = r_i^2 $

Next, I applied the above method to the example given in the question statement, where $\mathbf{p_1} = (2, 3)$, $\mathbf{p_2} = (12,9)$, $\mathbf{p_3} = (5, 17)$, and using $\dfrac{b}{a} = \dfrac{2}{3} $ and $\theta = 60^\circ$. The ellipse I got was as follows. It is identical to the one obtained with the method outlined in the question statement. Many thanks to @David K for his idea.