Circle inscribed in a semicircle

Question

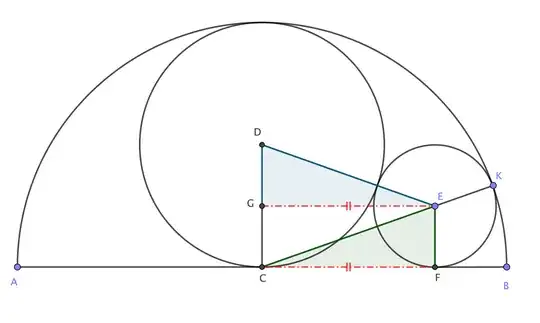
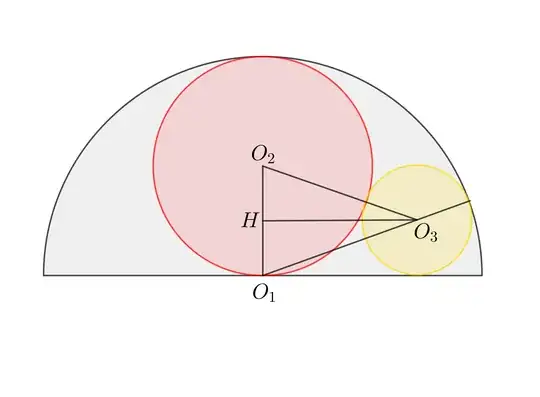
There is black semicircle, which radius is $ R $. The red circle is tangentially inward to the semicircle and to the diameter in its center. The yellow one is tangent externally to the red circle, internally to the semicircle and tangent to the diameter of the semicircle.

My question is :

What is the relationship between $R$ and the radius $r$ of yellow one?

My attempts :

I tried to use similarity of triangles, but always I had the third unknown number and two equations. I am sure that the radius of the red one is $ 0.5R$

Answer 1

Let the radius of the "black" semicircle be $[CK]=2R$. Thus, the radius of the "red" circumference will be $[DC]=R$. In virtue of the Pythagorean Theorem in the triangles $\triangle DGE$ and $\triangle ECF$ respectively

\begin{align*} GE^2=CF^2&=DE^2-DG^2=(R+r)^2-(R-r)^2=4Rr\\ &=CE^2-EF^2=(2R-r)^2-r^2=4R^2-4Rr\end{align*} Hence

$$4Rr=4R^2-4Rr\iff \color{blue}{2r=R}$$

The radius of the yellow circumference is, consequently, one-fourth of the radius of the black circle.

Answer 2

Consider a coordinate system with origin $O$ at the center of the semicircle. Let $(x,y)$ be the coordinate of the center $O'$ of a circle of radius $r$ that is tangent to the semicircle and its diameter. The distance $OO'$ equals $R- r$. Moreover, we have $y=r$. With Pythagoras we get $$(R-r)^2 = x^2 + r^2$$ and from that we get $$x^2 = R^2 - 2 R r$$

Now let $C_1$, $C_2$ two circles with centers $O_1$ $O_2$ that are tangent to the semicircle, to its diameter and moreover are tangent to each other. We have $O_1 O_2 = r_1 + r_2$. With Pythagoras again we get $$(r_1 + r_2)^2 = (x_1 - x_2)^2 + (r_1 - r_2)^2$$ and from here

$$2 x_1 x_2 = x_1^2 + x_2^2 - 4 r_1 r_2$$

Now raise to the square, using the equalities $x_i^2 = R^2 - 2 R r_i$ and we get, $$(r_1^2 - 6 r_1 r_2 + r_2^2) R^2 + 4 (r_1^2 r_2 + r_1 r_2^2)R + 4 r_1^2 r_2^2==0$$ and so $$r_2 = \frac{ 3 R^2 r_1 - 2 R r_1^2 \pm 2\sqrt{2} R r_1 \sqrt{R(R-2 r_1)} } {(R+2 r_1)^2}$$

In particular, for $R=1$, and $r_1=1/2$, we get $r_2=1/4$.

Answer 3

HINT

Consider the Figure below and note that

1. $\overline{O_2H} = \frac{R}{2}-r$;
2. $\overline{O_2O_3} = \frac{R}{2} + r$;
3. $\overline{HO_1} = r$;
4. $\overline{O_1O_3} = R-r$;

Use Pythagorean theoerm on $\triangle O_2HO_3$ and on $\triangle O_1HO_3$ to determine $\overline{HO_3}$ in two ways and thus get an equation, which, once solved, will give you the desider result of $r$ as a function of $R$.