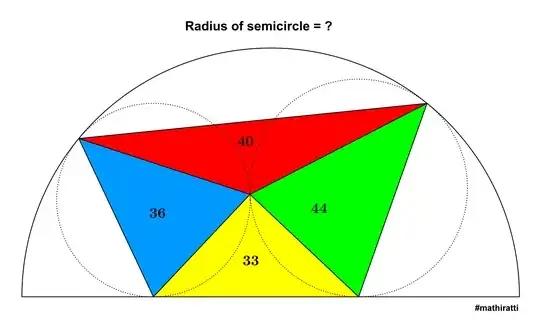
Two circles inscribed in a semicircle

Question

Two circles are inscribed in a semi circle. Given the areas of the shaded triangles, what's the radius of the semicircle? (Note there's a similar but different question here)

Answer 1

It's not easy to believe, but by pure luck, the solution is found as:

\begin{align} R&=\frac67\sqrt{187\sqrt2}\approx 13.939 ,\\ r_1&=\frac13\sqrt{187\sqrt2}\approx 5.42 ,\\ r_2&=\frac38\sqrt{187\sqrt2}\approx 6.0983 . \end{align}

Edit

$\require{begingroup} \begingroup$ $\def\i{\cdot\mathbf{i}}$

I just started to build the construction from two radii of inscribed circles, and it was a pure stroke of luck: a pair $r_1=8,\ r_2=9$ looks nice to start with. When the inradii are known, the radius of semicircle $R$ can be easily found as

\begin{align} R&= \frac{2r_1 r_2(r_1+r_2+2\sqrt{2r_1 r_2})}{6r_1 r_2-r_1^2-r_2^2} . \end{align}

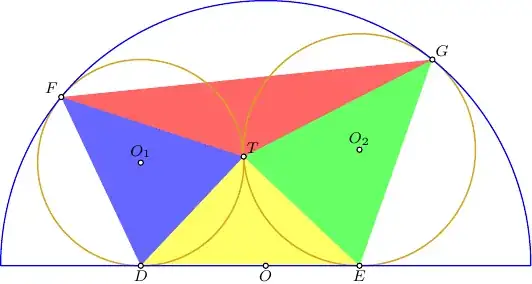
Using complex numbers to express coordinates of the points, we have:

\begin{align} O&=0 \\ ,\quad O_1&= O-\sqrt{(R-r_1)^2-r_1^2}+r_1\i =-\tfrac{48}7\sqrt2+8\i ,\\ O_2&= O+\sqrt{(R-r_2)^2-r_2^2}+r_2\i =\frac{36}7\sqrt2+9\i ,\\ D&=O_{1x}=-\frac{48}7\sqrt2 ,\\ E&=O_{2x}=\frac{36}7\sqrt2 ,\\ F&=O_1+r_1\cdot\frac{O_1-O}{|O_1-O|} =-\frac{864}{77}\sqrt2+\frac{144}{11}\i ,\\ G&=O_2+r_2\cdot\frac{O_2-O}{|O_2-O|} =\frac{64}7\sqrt2+16\i ,\\ T&=O_1+r_1\cdot\frac{O_2-O_1}{|O_2-O_1} =-\frac{144}{119}\sqrt2+\frac{144}{17}\i . \end{align}

Given these known points, the corresponding areas are

\begin{align} s_1=S_{TFD}&=\frac{10368}{187}\sqrt2 =\frac{288}{187}\sqrt2\cdot 36 ,\\ s_2=S_{TDE}&=\frac{864}{17}\sqrt2 =\frac{288}{187}\sqrt2\cdot 33 ,\\ s_3=S_{TEG}&=\frac{1152}{17}\sqrt2 =\frac{288}{187}\sqrt2\cdot 44 ,\\ s_4=S_{TGF}&=\frac{11520}{187}\sqrt2 =\frac{288}{187}\sqrt2\cdot 40 , \end{align}

so the solution was obvious.

$\endgroup$

Answer 2

I must say that the first contact with this question left me so perplexed that I asked a question about one of the interrogations I had.

The answers you will find there should be read before embarking into the following solution.

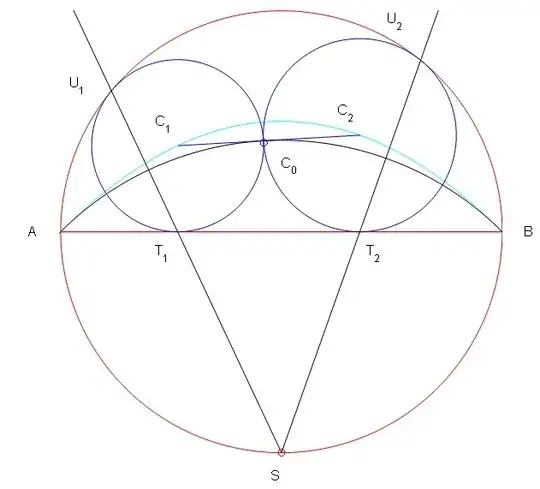
Let us begin by a certain number of notations that can be followed on figure 1.

Fig. 1. $C_0$ belongs to the circle with center $S(0,-r)$ and radius $r \sqrt{2}$. $C_1$ and $C_2$ belong to parabola $(P)$ (light blue) with equation $y=\dfrac{1}{2r}(r^2-x^2)$.

Consider the two little circles. Let $C_1(x_1,y_1)$, $C_2(x_2,y_2)$ be their resp. centers. Let $C_0(x_0,y_0)$ be their tangency point. As a consequence, the tangency points on the diameter are $T_1(x_1,0)$, $T_2(x_2,0)$. The other tangency points being, for $k=1,2$:

$$U_k \left(x'_k=\dfrac{2r^2x_k}{r^2+x_k^2}, \ y'_k=r \dfrac{r^2-x_k^2}{r^2+x_k^2}\right)\tag{1}$$

due to the fact that $S,T_k,U_k$ are aligned.

We are going to show that it is possible to write the constraints in terms of the three parameters, ultimately with the single parameter $y_0$. What are these constraints ?

a) $C_0$ belongs to the circle with center $S$ and radius $r \sqrt{2}$. Therefore:

$$x_0^2+y_0^2+2ry_0-r^2=0\tag{2}$$

giving:

$$x_0=-\sqrt{2r^2-(y_0+r)^2}\tag{2'}$$

(please note the minus sign in front of the square root, chosen in order to enforce condition $x_0<0$ which is the same as saying that the smaller circle is on the left of the bigger one).

b) The equation of the tangent line to conic curve $(P)$ in $(x_0,y_0)$ is obtained from (2) as:

$$xx_0+yy_0+r(y+y_0)-r^2=0\tag{2''}$$

As $C_1$ and $C_2$ are the intersection points of this straight line with parabola (P), their abscissas $x_1$ and $x_2$ will be the roots of the quadratic equation obtained by plugging $y=\dfrac{1}{2r}(r^2-x^2)$ in ($2'*$). Rather easy calculations give:

$$\begin{cases}x_1&=&r\dfrac{x_0-\sqrt{2}y_0}{r + y_0},\\ x_2&=&r\dfrac{x_0+\sqrt{2}y_0}{r + y_0}\end{cases}\tag{3}$$

A direct consequence of (3) is that:

$$x_0-x_1=y_0\dfrac{r\sqrt{2} + x_0}{r+y_0}\tag{4}$$

Our first goal has been achieved.

It's time now to involve the information about the areas. We will consider the blue and yellow areas with resp. values $33$ and $36$:

The area of the blue triangle is clearly ("half base times height"):

$$\frac12(x_2-x_1)y_0=33$$

Using (3), we can transform it into:

$$\dfrac{\sqrt{2}y_0^2r}{r+y_0}=33 \ \iff \ r=\dfrac{33y_0}{\sqrt{2} y_0^2 - 33}\tag{5}$$

Besides, the area of the yellow triangle $C_0U_1T_1$ (we have described the triangle with a positive orientation) can be expressed under the following determinant form:

$$\tfrac12 \begin{vmatrix}x_0&x'_1&x_1\\ y_0&y'_1&0\\ 1&1&1\end{vmatrix}=\tfrac{1}{2 (r^2+x_1^2)} \begin{vmatrix}x_0&2r^2x_1&x_1\\ y_0&r(r^2-x_1^2)&0\\ 1&(r^2+x_1^2)&1\end{vmatrix}=\tfrac{1}{2 (r^2+x_1^2)} \begin{vmatrix}x_0-x_1&2r^2x_1&x_1\\ y_0&r(r^2-x_1^2)&0\\ 0&(r^2+x_1^2)&1\end{vmatrix}$$

(we have used formulas (1) and replaced column 1 by the difference between column 1 and column 3), giving rise to the following equation: $$ \begin{vmatrix}x_0-x_1&2r^2x_1&x_1\\ y_0&r(r^2-x_1^2)&0\\ 0&(r^2+x_1^2)&1\end{vmatrix}=2 (r^2+x_1^2) 36\tag{6}$$

in which $x_0-x_1$ can be replaced by its expression in (4).

We have now the possibility to deduce from all these equations, by "cascade substitutions" a polynomial equation in $y_0$ (that I haven't explicited, using a CAS for these last computations: see remark below). This equation gives the only possible solution in conformity with the figure:

$$y_0=6\sqrt{\dfrac{11 \sqrt{2}}{17}}\approx 5.7396$$

from which, using (5), we get:

$$r=\dfrac67\sqrt{187\sqrt{2}}\approx 13.9390$$

(which is the same value as that found by g.kov).

Remarks: One could object that we haven't used the two other values of the two other triangles. I must say that I haven't attempted to use them because

1. I was tired by all these endless calculations [not entirely done by hand; I have relied for the final computation upon the Computer Algebra System available under the Matlab environment].

2. One can await that the two other values attest the values already obtained. Otherwise... one could question the author... Besides, what is the origin of this problem ?

Answer 3

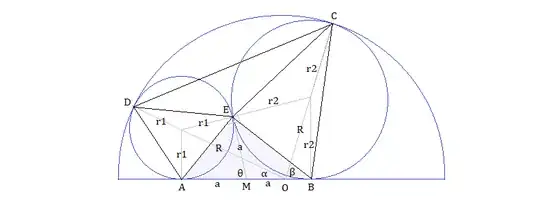
Let $EM=a$ be tangential to both circles at the point $E$ and the angle $\theta$. Then, the area $[ABE] = 33= a^2\sin\theta$ and

\begin{align} [ABCD]&=153 =[AOD]+[BOC]=[COD] \\ & = \frac12Rr_1\cos\alpha + \frac12Rr_2\cos\beta + \frac12R^2\sin(\alpha+\beta) \end{align} Substitute $\sin\alpha = \frac{r_1}{R-r_1}$, $\sin\beta= \frac{r_2}{R-r_2}$ into above equation and, after simplifing \begin{align} 153=aR\left( \frac1{(1-\frac{r_1}{R})(1-\frac{r_2}{R})}-1\right)\tag1 \end{align}

Note that $r_1 = a \tan\frac{\theta}2$, $r_2 = a \cot\frac{\theta}2$ and $AB=AO +OB$, or \begin{align} 2a & = \sqrt{(R-r_1)^2-r_1^2} + \sqrt{(R-r_2)^2-r_2^2} = \sqrt{R^2-2aR\tan\frac{\theta}2}+ \sqrt{R^2-2aR\cot\frac{\theta}2} \end{align} which reduces to $$R = \frac a{\sqrt2-\csc\theta}$$

Then, along with $a^2=33\csc\theta$, substitute $r_1$, $r_2$ and $R$ derived above into (1) to obtain the equation for $\theta$ $$\frac{153}{33} = \frac{\csc\theta}{\sqrt2-\csc\theta}\left(\frac1{3-4\sqrt2\csc\theta+3\csc^2\theta} -1\right) $$ Solve to get the valid solution $\csc\theta = \frac{17}{12\sqrt2}$ and, in turn, the radius

$$R = \frac{\sqrt{33\csc\theta}}{\sqrt2-\csc\theta} = \frac67\sqrt{187\sqrt2}$$

Answer 4

Here is a second solution, based on simpler considerations than the first one, involving in particular the concept of power of a point with respect to a circle.

I still refer, for some properties of this problem to this question of mine and its answers containing in particular the following results (see Fig. 1):

• Tangency point $C_0(x_0,y_0)$ belongs to the (black) circle $(C)$ with center $S(0,-r)$ and radius $r \sqrt{2}$, with equation:

$$x_0^2+y_0^2+2ry_0-r^2=0\tag{0}$$

Therefore:

$$x_0^2+y_0^2+2ry_0-r^2=0\tag{1}$$

• Centers of circles (either $C_1$ or $C_2$) belong to parabola $(P)$ (light blue) with equation:

$$y=\dfrac{1}{2r}{(r^2-x^2)}\tag{2}$$

• Points $S,T_1,U_1$, and $S,T_2,U_2$ are aligned.

Fig. 1.

Let $C_1(x_1,y_1)$, $C_2(x_2,y_2)$ be the resp. centers of the two small circles with $x_1<x_2$. As a consequence, the tangency points on diameter $AB$ are $T_1(x_1,0)$, $T_2(x_2,0)$.

The equation of the tangent line to circle $(C)$ in $(x_0,y_0)$ is obtained from (0):

$$xx_0+yy_0+r(y+y_0)-r^2=0\tag{3}$$

As $C_1$ and $C_2$ are the intersection points of this straight line with parabola (P), their abscissas $x_1$ and $x_2$ are the roots of the quadratic equation obtained by plugging $y=\dfrac{1}{2r}(r^2-x^2)$ in ($3$). Rather easy calculations give:

$$\begin{cases}x_1&=&r\dfrac{x_0-\sqrt{2}y_0}{r + y_0},\\ x_2&=&r\dfrac{x_0+\sqrt{2}y_0}{r + y_0}\end{cases}\tag{3}$$

Now, let us use the so-called power of point $T_1$ with respect to the (red) circle with center $(0,0)$ and radius $r$.

$${\frak P}(T_1)=-(T_1U_1).(T_1 S)=-(T_1A).(T_1B) \ \implies \ T_1U_1=\dfrac{r^2-x_1^2}{\sqrt{r^2+x_1^2}}\tag{4}$$

Besides, if we denote by $F_1$ the foot of the altitude issued from $C_0$ in triangle $C_0U_1T_1$, we get (using a classical formula for the distance of a point to a straight line):

$$C_0F_1=\dfrac{|rx_0-x_1(y_0+r)|}{\sqrt{r^2+x_1^2}}$$

As a consequence, the area of triangle $C_0U_1T_1$ can be expressed in two ways ("half base times height" on the LHS, given value on the RHS), yielding the following equation:

$$\frac12\frac{(r^2-x_1^2)}{\sqrt{r^2+x_1^2}}\frac{(r x_0-r x_1 - x_1 y_0)}{\sqrt{r^2+x_1^2}}=36$$

which is equivalent to:

$$(r^2-x_1^2)(r x_0-r x_1 - x_1 y_0)=72(r^2+x_1^2)\tag{5}$$

In a symmetric way, one gets for the other triangle $C_0U_1T_2$:

$$-(r^2-x_2^2)(r x_0-r x_2 - x_2 y_0)=88(r^2+x_2^2)\tag{6}$$

(the minus sign in front of the LHS accounts for the fact that this triangle is negatively oriented).

Finally, the area of the blue triangle gives rise to equation:

$$\frac12(x_2-x_1)y_0=33\tag{7}$$

We have now the possibility to deduce from equations (3),(1),(5),(6) and (7), by "cascade substitutions", the value of $r$. These computations haven't been explicited because I chose to use the CAS (Computer Algebra System) associated with Matlab for these last computations. Here is the Matlab program I have written:

 syms r x0 y0 x1 x2
 x1= r*(-2^(1/2)*y0 + x0)/(r + y0);
 x2= r*( 2^(1/2)*y0 + x0)/(r + y0);
 [R,X0,Y0]=solve(x0^2+y0^2+2*r*y0-r^2==0,...
          (r^2-x1^2)*(r*x0-r*x1-x1*y0)==72*(r^2+x1^2),...
          (r^2-x2^2)*(r*x0-r*x2-x2*y0)==-88*(r^2+x2^2),...
           (x2-x1)*y0==66,...
          'Real',true,...
           r,x0,y0)

giving in particular:

$$r=\dfrac67\sqrt{187\sqrt{2}}\approx 13.9390 \ \ \ \text{and} \ \ \ y_0=6\sqrt{\dfrac{11 \sqrt{2}}{17}}\approx 5.7396$$

($r$ has the same value as that found by g.kov).

Remark: we haven't used the area value $40$ of the red triangle.