2

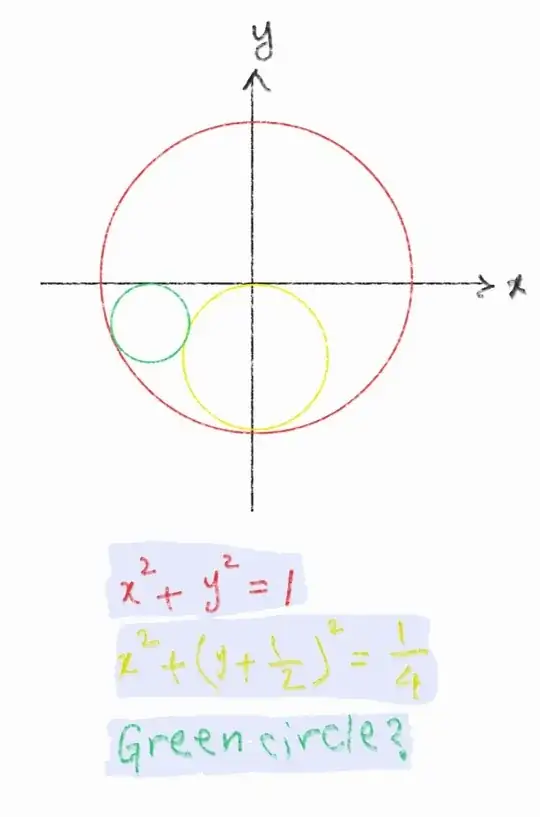
Given two circles:

$\color{red}{\Gamma_1: x^2+y^2=1}$

$\color{blue}{\Gamma_2: x^2+(y+\frac{1}{2})^2=\frac{1}{4}}$

$\color{green}{\Gamma_3: \dots ?}$

where $\color{green}{\Gamma_3}$ touchs $\color{red}{\Gamma_1}$ and $\color{blue}{\Gamma_2}$, and lies in the $3^\text{rd}$ quadrant.

Can we, without trigonometry, find the equation of $\color{green}{\Gamma_3}$?

My concern is to find the radius, without trigonometry, or at least to bound it from above and bellow as best as we can.

My bad estimation is $0<\color{green}{r}<\frac{1}{2}$ because it smaller than $\color{blue}r$. Can we find a better bounds?

Rough sketch: enter image description here

I do not need solutions, I need key ideas, then I can provide my attempts according to the key ideas.

Your help would be appreciated. THANKS!

Hussain-Alqatari
  • 5,738
  • 3
  • 16
  • 44
  • Join the centres of $\Gamma_1$, $\Gamma_2$ and $\Gamma_3$ to form a triangle; the three sides have lengths $\frac12$, $\frac12+r_3$ and $1-r_3$. The centre of $\Gamma_3$ also has a $y$-coordinate equal to $-r_3$. – peterwhy Mar 28 '24 at 23:00
  • 1
    [Spoiler Alert] The radius is calculated here. – User Mar 28 '24 at 23:02

0 Answers0