9

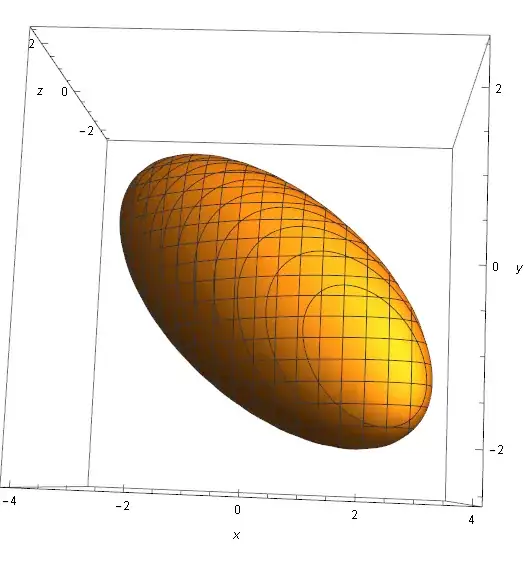
Take the following ellipsoid in implicit form as an example:

$$x^2 + 2 y^2 + 3 z^2 + x y + y z - 2 xz = 5$$

which shows:

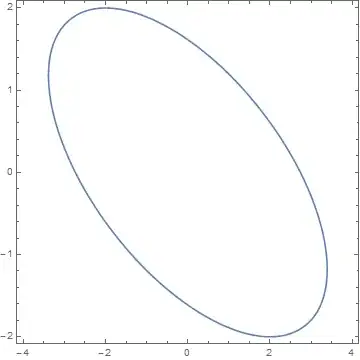
enter image description here

The parallel projection of the ellipsoid onto $xoy$ coordinate plane can be obtained as:

$$ 8 x^2 + 16 x y+23 y^2=60$$

enter image description here

Is it possible to prove:

  1. The parallel projection of an ellipsoid is always an ellipse and how?

I guess this should be able to be generalized into:

  1. the perspective projection of an ellipsoid is a conic curve.

How to prove it?

In prjective geometry, the quadratic form of conics is useful in such proof. This one seems a little more difficult.

Rodrigo de Azevedo
  • 23,223
user6043040
  • 712
  • 2
    A plane is defined by a vector $\mathbf{v}$ and a displacement $b$, ie $f(\mathbf{x}) = \mathbf{v}\cdot\mathbf{x}-b = 0$. The parallel projection amounts to removing any extension/support in the $\mathbf{v}$ direction. An ellipse can be parametrised in terms of its 3 principle axes and its axis lengths so you could transform into that representation and then apply a projection operator on each axis and, hopefully, you end up with the parametrisation for the interior and boundary of a 2d ellipse. It's a general approach, I think, but seems somewhat inelegant. Doesn't answer Part 2 either. – AlphaNumeric Jul 20 '16 at 10:01
  • 1
    I have shown in my answer to this question : (https://math.stackexchange.com/q/2438495) that there is a connection with a certain Schur complement of the matrix of the ellipsoid. – Jean Marie Nov 25 '17 at 16:23
  • It suffices to prove this for the unit sphere, since the general case can be transformed into this by an affinity. – amd Oct 03 '18 at 23:23

1 Answers1

7

$\newcommand{\dd}{\partial}$No claim of elegance, but Cartesian coordinates handle both questions, and the answers are "yes":

Up to translation, a general ellipsoid can be written in the form $$ Ax^{2} + By^{2} + Cz^{2} + 2(Dxy + Exz + Fyz) = 1 \tag{1} $$ for some positive-definite coefficient matrix $$ \left[\begin{array}{@{}ccc@{}} A & D & E \\ D & B & F \\ E & F & C \\ \end{array}\right]. $$

  1. For definiteness, project the ellipsoid to the $(x, y)$-plane along the $z$-axis, and call the image the shadow. A point $p = (x, y, z)$ on the ellipsoid projects to the boundary of the shadow if and only if the tangent plane to the ellipsoid at $p$ is parallel to the $z$-axis, if and only if $$ 0 = \frac{\dd}{\dd z}\bigl(Ax^{2} + By^{2} + Cz^{2} + 2(Dxy + Exz + Fyz)\bigr) = 2(Ex + Fy + Cz). $$ That is, the boundary of the ellipsoid's shadow is the shadow of a plane section of an ellipsoid (an ellipse), hence itself an ellipse.

  2. Let $p_{0} = (x_{0}, y_{0}, z_{0})$ be an arbitrary point outside the ellipsoid. The ray from $p_{0}$ to a point $p = (x, y, z)$ on the ellipsoid is tangent to the ellipsoid if and only if the normal to the ellipsoid at $p$ is orthogonal to the ray, if and only if $$ \nabla\bigl(Ax^{2} + By^{2} + Cz^{2} + 2(Dxy + Exz + Fyz)\bigr) \cdot (p - p_{0}) = 0, $$ or (after dividing by $2$) $$ (Ax + Dy + Ez)(x - x_{0}) + (Dx + By + Fz)(y - y_{0}) + (Ex + Fy + Cz)(z - z_{0}) = 0. \tag{2} $$ After expanding, the second-order terms are precisely the left-hand side of (1); that is, (2) is again a linear equation. Consequently, the "horizon" of the ellipsoid from an arbitrary exterior center of projection is a plane section, so it projects to a (possibly degenerate) ellipse regardless of the "screen" plane.

Andrew D. Hwang
  • 82,053