3

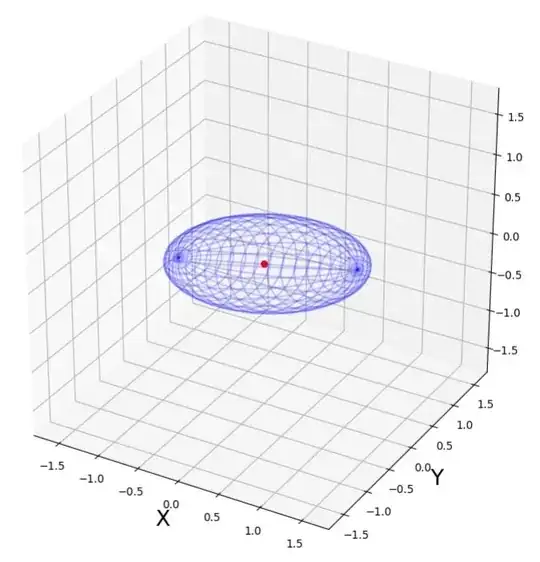
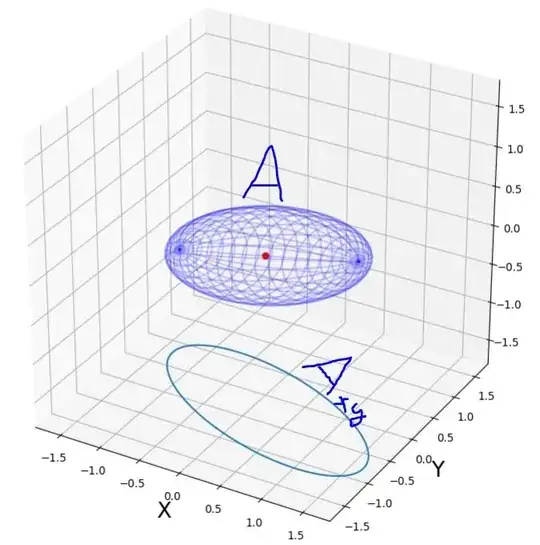
Suppose we have a $N\times N$ symmetric-positive-definite matrix $A$, representing an ellipsoïd in $N$ dimensional space. How to find the matrix $A_{xy}$ corresponding to orthogonal projection of ellispoid on $xy$-plan ?

I have already consulted this pages, they were not that helpful:

How to obtain the equation of the projection/shadow of an ellipsoid into 2D plane? https://math.stackexchange.com/a/1866994/1054066

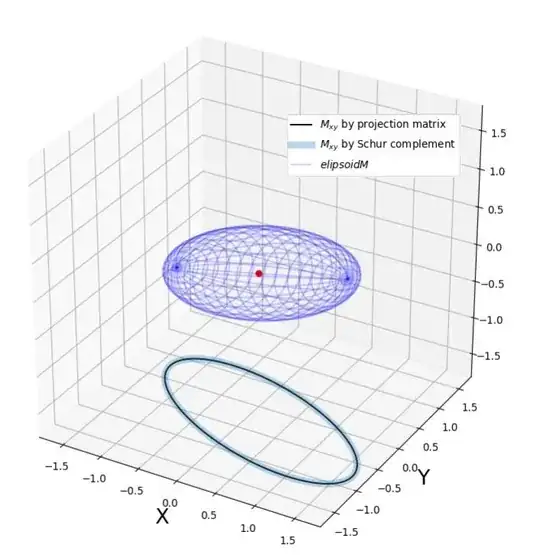
edit after some suggestions : Schur complement method seems to work in 3 dimensions:

here's an exemple:

suppose $A = \begin{pmatrix} 1 & 0.5 & -1 \\ 0.5 & 2 & 0.5 \\ -1 & 0.5 & 3 \end{pmatrix}$

enter image description here

than Schur complement method says that $A_{xy} = \begin{pmatrix} 1 & 0.5 \\ 0.5 & 2\end{pmatrix} - \frac{1}{3} \begin{pmatrix} -1 \\ 0.5\end{pmatrix} \begin{pmatrix} -1 & 0.5\end{pmatrix} = \begin{pmatrix} 0.67 & 0.67 \\ 0.67 & 1.92\end{pmatrix}$

Here's the result :

enter image description here

but I dont see how to make it work in 5 dimansional space. The goal is to project 5D-ellipsoid on xy-plane.

Artashes
  • 195
  • 2
    Take a look at the answer I gave here which amounts to say that you have to take the $2 \times 2$ "Schur's complement" (corresponding to the pair of variables of the plane you want to project onto) in the $n \times n$ matrix $A$. – Jean Marie May 03 '22 at 12:35
  • @JeanMarie I have tried to use Schur's complement method but it doesn't seem to work. I edited my post showing an exemple. – Artashes May 04 '22 at 10:05
  • I am going to have a look at your computations. Any Schur's complement issued from a positive definite matrix should be definite positive... – Jean Marie May 04 '22 at 10:14
  • I see a first problem: your $3 \times 3$ matrix isn't symmetric... – Jean Marie May 04 '22 at 10:15
  • @JeanMarie, sorry it's a typo, actually the matrix is symmetric, I didn't copy it correctly here. – Artashes May 04 '22 at 11:47

1 Answers1

1

Suppose M is a symmetric $N \times N$ matrix representing an ellipsoid : $$X^T M X = 1$$ with $X \in \mathbb{R}^N$.

1st method of projection : using a projection matrix P $$P_{xy} = \begin{pmatrix} 1 & 0 & 0 & ... & 0 \\ 0 & 1 & 0 & ... & 0\end{pmatrix} = \begin{pmatrix} \overrightarrow{i} \\ \overrightarrow{j} \end{pmatrix}$$ where $\overrightarrow{i}$ and $\overrightarrow{j}$ cartesian base vectors for $xy$-plane. For exemple if we want to project an object of 7-dimensional to 3-dimensional space (on any 3 arbitrary axis) than the projection matrix will take the form : $$ P_{7D \to 3D} = \begin{pmatrix} 1&0&0&0&0&0&0 \\ 0&0&0&0&1&0&0 \\ 0&0&1&0&0&0&0 \end{pmatrix} = \begin{pmatrix} \overrightarrow{e_1} \\ \overrightarrow{e_5}\\ \overrightarrow{e_3} \end{pmatrix}$$

The projection of M on $xy$-plane is an ellipse given by $M_{xy}$ : $$ M_{xy} = (P_{xy} M^{-1} P_{xy}^T)^{-1} $$

2nd method : using the Schur complement.

First we divide the matrix M into 4 blocs as follows : $$ M = \begin{pmatrix} A & B \\ D & C \end{pmatrix}$$ than Schur's complement gives $M_{xy}$ :

$$ M_{xy} = A - BC^{-1}D $$

here's an exemple :

$$ M = \begin{pmatrix} 1 & 0.5 & -1 \\ 0.5 & 2 & 0.5 \\ -1 & 0.5 & 3 \end{pmatrix}$$

1st method: projection matrix $$P_{xy} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix}$$

$$M_{xy} = (P_{xy} M^{-1} P_{xy}^T)^{-1} = \begin{pmatrix} 0.67 & 0.67 \\ 0.67 & 1.92\end{pmatrix}$$

2nd method : Schur complement $$M_{xy} = \begin{pmatrix} 1 & 0.5 \\ 0.5 & 2 \end{pmatrix} - \begin{pmatrix} -1 \\ 0.5 \end{pmatrix} \frac{1}{3} \begin{pmatrix} -1 & 0.5 \end{pmatrix} = \begin{pmatrix} 0.67 & 0.67 \\ 0.67 & 1.92\end{pmatrix}$$

enter image description here

Artashes
  • 195
  • In the case of $5 \times 5$ matrix, partition it into $M = \begin{pmatrix} A & B \ D & C \end{pmatrix}$ where now $S=A-DC^{-1}B$ with $A,C$ with dimensions $2 \times 2$ and $3 \times 3$ resp. – Jean Marie May 04 '22 at 17:16
  • @JeanMarie, I finally got the results – Artashes May 04 '22 at 18:58