This tag is for questions relating to Eulerian paths in graphs. An "Eulerian path" or "Eulerian trail" in a graph is a walk that uses each edge of the graph exactly once. An Eulerian path is "closed" if it starts and ends at the same vertex.
In graph theory, the study of an Eulerian trail (or Eulerian path) came up in their relation by Leonhard Euler while solving the famous Seven Bridges of Königsberg problem in 1736.
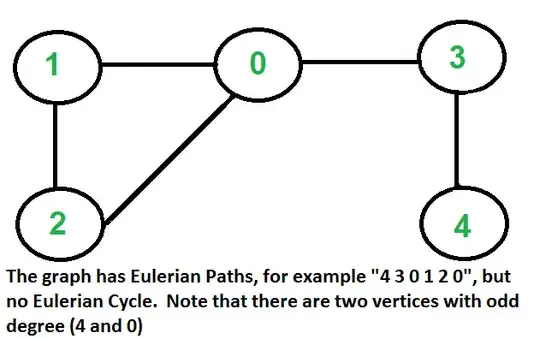
An Eulerian path is a trail in a graph which visits every edge exactly once.
For the existence of Eulerian trails it is necessary that zero or two vertices have an odd degree. If there are no vertices of odd degree, all Eulerian trails are circuits. If there are exactly two vertices of odd degree, all Eulerian trails start at one of them and end at the other. A graph that has an Eulerian trail but not an Eulerian circuit is called semi-Eulerian.
Example:
- The Euler Circuit (when the starting vertex of the Euler path is also connected with the ending vertex of that path) is a special type of Euler path.
Applications: Eulerian trails are used in bioinformatics to reconstruct the DNA sequence from its fragments. They are also used in CMOS circuit design to find an optimal logic gate ordering. There are some algorithms for processing trees that rely on an Euler tour of the tree (where each edge is treated as a pair of arcs). The Gray code used for error detection and correction can be constructed as an Eulerian trail of de Bruijn graphs.
Reference: