Generally,the length of the sum of two vectors is not equal to the sum of their lengths. To see this consider the vectors $u$ and $v$ as shown below.
By considering $u$ and $v$ as two sides of a triangle, we can see that the lengths of the third side is $\| u + v \|$ and we have $\| u + v \| \leq \|u\| + \|v\|$. Under what circumstance equality occurs and how can one prove that?
I have noticed that the answer has been written down in the comments. Just to have an answer I am writing this one down.
Consider $\|u+v\|^2=(u+v) \cdot (u+v)$ where $u \cdot v$ represents the standard inner product/scalar product.Therefore $$\|u+v\|^2=\|u\|^2+2 (u \cdot v) + \|v\|^2 .$$
By the Cauchy-Schwarz Inequality we have $$u \cdot v \leq \|u\| \cdot \|v\|.$$
So, $$\|u+v \|^2= \|u\|^2+2(u \cdot v)+ \|v \|^2 \leq \|u\|^2+ 2 \|u\| \cdot \|v\| + \|v\|^2=(\|u\|+ \|v\|)^2 ,$$ i.e., $$\|u+v\|^2 \leq (\|u\|+ \|v\|)^2 \implies \|u+v\| \leq \|u \|+ \|v\| .$$
The Cauchy-Schwarz Inequality holds for any inner Product, so the triangle inequality holds irrespective of how you define the norm of the vector to be, i.e., the way you define scalar product in that vector space.
In this case, the equality holds when vectors are parallel i.e, $u=kv$, $k \in \mathbb{R}^+$ because $u \cdot v= \|u \| \cdot \|v\| \cos \theta$ when $\cos \theta=1$, the equality of the Cauchy-Schwarz inequality holds.
I always like to see and prove this visually:
One can find $A$,$B$ and $C$ points on the plane such that
\begin{align*} \overrightarrow{AB}&={\overrightarrow{u}}\\ {\overrightarrow{BC}}&=\overrightarrow{v}\\ \overrightarrow{AC}&=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{u}+\overrightarrow{v}. \end{align*}
Now fix points $A$ and $B$.
The questions that arise are the following: if we could move C to another position C', how should we move it such that:
In other words, how should we rotate the vector $\overrightarrow{v}={\overrightarrow{BC}}$ around B such that the distance $\lvert\overrightarrow{u}+\overrightarrow{v}\rvert=\lvert\overrightarrow{AC}\rvert$ from $A$ to $C$ maximizes? What will be the max value?
The answer to $(1)$ are all the points $C'$ in the plane belonging to the circle with centre B and radius $\lvert{\overrightarrow{BC'}}\rvert=\lvert{\overrightarrow{v}}\rvert$.
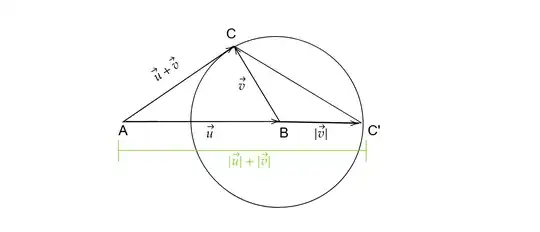
Geometrically, the answer to $(2)$ seems to be the point $C'$ in the figure.
If this is the case, then the answer to (3) is obvious: $$\lvert{\overrightarrow{AC'}}\rvert=\lvert{\overrightarrow{AB}+\overrightarrow{BC'}}\rvert=\lvert{\overrightarrow{AB}}\rvert+\lvert{\overrightarrow{BC'}}\rvert =\lvert{\overrightarrow{u}}\rvert+\lvert{\overrightarrow{v}}\rvert.$$ But why $C'$ in the figure is the right point?
We can use simple arguements from Euclidean Geometry to prove this arguement: For the triangle $\triangle C'BC$ we have $\lvert{\overrightarrow{BC}}\rvert=\lvert{\overrightarrow{BC'}}\rvert$, hence the angles $\widehat{BC'C}=\widehat{BCC'}$ will be equal. We also have $\widehat{BCC'}\leq \widehat{ACC'}$, hence $\widehat{AC'C}=\widehat{BC'C}=\widehat{BCC'}\leq \widehat{ACC'}$. The last inequality holds for the triangle $\triangle ACC'$, and so the same inequality will hold for the segments that are opposite to these angles on that triangle: $$\widehat{AC'C}\leq \widehat{ACC'}\implies \lvert{\overrightarrow{AC}}\rvert\leq \lvert{\overrightarrow{AC'}}\rvert.$$ Particularly, it holds that \begin{align*} \lvert{\overrightarrow{u}+\overrightarrow{v}}\rvert&=\lvert{\overrightarrow{AB}+\overrightarrow{BC} }\rvert\\ &=\lvert{\overrightarrow{AC}}\rvert\\ &\leq \lvert{\overrightarrow{AC'}}\rvert\\ &=\lvert{\overrightarrow{AB}}\rvert+\lvert{\overrightarrow{BC'}}\rvert\\ &=\lvert{\overrightarrow{AB}}\rvert+\lvert{\overrightarrow{BC}}\rvert\\ &=\lvert{\overrightarrow{u}}\rvert+\lvert{\overrightarrow{v}}\rvert \end{align*} which is exactly the triangle inequality and the reason that is called that way.
