5

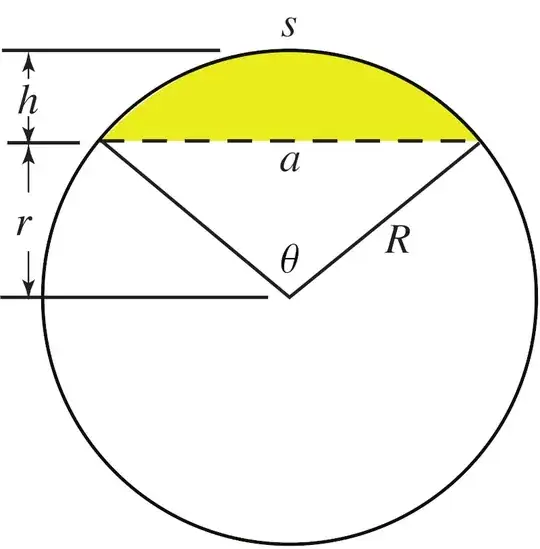
Please imagine that we have a circular segment with some arc length 's' and chord length 'a' (using notation from http://mathworld.wolfram.com/CircularSegment.html):

circular segment

Provided only 'a' and 's', and placing the left-hand-side point of the chord at the origin of the Euclidean plane (or a more convenient point), is there sufficient information to write an expression for the height of the circular segment (i.e. the y-axis/"vertical" distance between the chord on the x-axis and the circular arc) as a function of a position on the chord?

It's a simple matter to express the chord length in terms of the arc length and theta: $a = (s) * 2\frac{\sin(\frac{\theta}{2})}{\theta}$, or an expression for the arc length in terms of the chord length and theta: $s = \frac{a\theta}{2\sin\frac{\theta}{2}}$. And one can write an express for the maximum height as: $h = R - \frac{1}{2}\sqrt{(-a)^2+4R^2}$, where the radius of the circle, 'R' is related to theta as: $R = \frac{1}{2} \sqrt{\frac{a^2}{\cos^2\frac{\theta}{2}-1}}$.

If there is insufficient information to accomplish the above, I would love to have an intuitive explanation for why this is so.

Reinderien
  • 194
David
  • 95
  • With just $s$ and $a$, the problem is ill-posed. There's no way to determine the radius or other such useful info from just those two. – J. M. ain't a mathematician Nov 01 '10 at 02:35
  • I feel that we should be able to derive the curvature of the line segment from 's' and 'a'? And with that, reconstruct the circle? – David Nov 01 '10 at 02:39
  • Consider the further constraint that the arc segment must have constant curvature, and that we have two points we know the segment of the circular curve passes through. I feel intuitively the information is there for this calculation. – David Nov 01 '10 at 02:44
  • 1
    Remember that a chord divides a circle into a "small arc" and a "big arc" (tacitly excluding the case where the chord is a diameter). It should not be hard to find small arc-big arc pairs (the two implied circles are of different radii, of course) that have the same length. – J. M. ain't a mathematician Nov 01 '10 at 02:50
  • Circles have constant curvature, so that restriction is moot. – J. M. ain't a mathematician Nov 01 '10 at 02:51
  • J.M., the constant curvature point was a point about intuition not intended as a further restriction... – David Nov 01 '10 at 02:57

2 Answers2

6

Using the notation of the figure you have linked to, we have

\begin{equation} R \sin \frac{\theta}{2} = \frac{a}{2} \end{equation}

we can also write

\begin{equation} \theta = \frac{s}{R} = \frac{2 s \sin \theta/2}{a} \end{equation}

From this equation, you can solve for $\theta$.

Once you have solved for $\theta$, you have

\begin{equation} h = R - R \cos(\theta/2) \end{equation}

Since $R = a/(2 \sin \theta/2)$, we have

\begin{equation} h = \frac{a}{2 \sin \theta/2} \left( 1 - \cos\left(\frac{s \sin\theta/2}{a}\right)\right) \end{equation}

svenkatr
  • 6,065
  • ok. I just saw J.M's comment about small and big arcs. My solution implicitly assumes that the arc length $s$ is the length of smaller segment of the circle. If you consider the other possibility (that the length s is the length of the larger segment), the solution you will get is $ h = \frac{a}{2 \sin \theta/2} \left( 1 + \cos\left(\frac{s \sin\theta/2}{a}\right)\right)$ – svenkatr Nov 01 '10 at 02:58
  • Yes, apologies, we should assume that it is the smaller length of the circle! – David Nov 01 '10 at 02:59
  • I need this too. But in this solution, you give a height calculation including theta. Given only an arch length and a chord length (no radius) I don't know how to calculate theta. I tried deriving it myself, but arrived at an equality containing both cosine theta and theta squared, and I don't know how to solve it. – rumtscho Feb 08 '11 at 21:39
  • 1
    @rumtscho - You would have to solve for $\theta$ using the equation $\theta = \frac{2s \sin \theta/2}{a}$. $s$ and $a$ are known. You would solve for $\theta$ numerically in general. – svenkatr Feb 09 '11 at 04:57
  • 1
    With $\phi = \theta/2$ we get $h = \dfrac{a(1 - \cos \phi)}{2 \sin \phi} = \dfrac{a \sin \phi}{2 (1+\cos \phi)}$. – Paul Frost Jan 03 '20 at 13:03
0

As @svenkatr wrote in comments, you will need to solve for $\theta$ $$\theta = \frac{2s }{a}\sin \left(\frac{\theta }{2}\right)$$ Let $x=\frac{\theta }{2}$ and $k=\frac s a$. Use Taylor series around $x=0$ and power series reversion to obtain $$x=t+\frac{t^3}{40}+\frac{107 t^5}{67200}+\frac{3197 t^7}{24192000}+O\left(t^9\right)\quad \text{where}\quad t=\sqrt{\frac{6 (k-1)}{k} }$$

For illustration, for $k=3$, the above truncated series gives $$x=\frac{428627}{189000}=2.26787$$ while the solution is $2.27886$.

There is no problem to take as many terms as we wish. Using twice mor terms, for the example, we would obtain $x=2.27877$

Claude Leibovici
  • 289,558