0

My question is related to mechanical engineering where a steel beam expands due to temperature rise and buckles to one side forming an arc. I couldn't get an answer to this in engineering forum.

If I know only length of chord and length of arc, can I calculate the height "h"? I do not know radius of circle. Please see the picture:

chord arc height

N. F. Taussig
  • 79,074
tipo1000
  • 1
  • 2
    If you knew that the arc was circular, then you might want to look at expressions involving the sagitta but it is not obvious to me that you do know it must be circular. – Henry Jan 13 '25 at 11:45
  • 1
    https://math.stackexchange.com/questions/8487/calculating-the-height-of-a-circular-segment-at-all-points-provided-only-chord-a seems related – Henry Jan 13 '25 at 11:46
  • @Henry OP says 'I do not know radius of circle' so either it is given or it is assumed as a working approximation that the beam's shape is (close enough to) a circular arc. – CiaPan Jan 13 '25 at 12:43
  • You can draw the center of the circle and write the expressions of arc length, chord and height using the radius $r$ and the angle $\theta$. Then you recover $\theta$ and $r$ from $a$ and $c$ using the reciprocal of sinc. – Christophe Boilley Jan 13 '25 at 12:56

1 Answers1

3

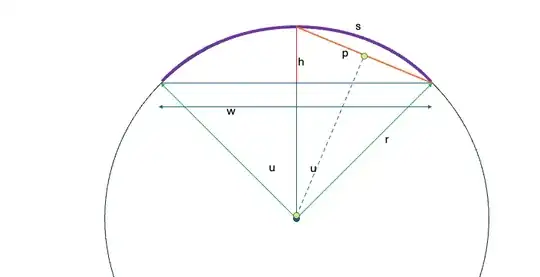
I'm guessing, from OP's "I don't know the radius" statement, that OP believes that the black curve is an arc of a circle. From this, we can solve the problem. Here's a figure with labels: diagram labeling the features of the problem

Known are $w$, the width of the chord, and $s$, the length of the arc. Unknown are the radius $r$ or the height $h$. Let's also call the angle between the two green rays $2u$ (measured in radians).

Then we know that $s = 2ru$. From trigonometry, we also know that $$ \sin(u) = \frac{w/2}{r} = \frac{w}{2r} = \frac{w}{s/u} = \frac{wu}{s}, $$ so $$ \frac{\sin(u)}{u} = \frac{w}{s}. \tag{1} $$ From this, we'll have to find $u$ numerically.

Now look at the isoceles triangle with the thick orange line as its base. The length of the orange line is $2r \sin(u/2)$ (a standard formula for length of a chord). We now have a right triangle with the orange segment as hypotenuse, $w/2$ as one leg, and the unknown $h$ as the other, so $$ h = \left( 4r^2 \sin^2(u/2) - \frac{w^2}{4} \right)^{\frac12}\tag{2} $$

Because, from equation 1, we know $u$, every term in equation 2 is now a known quantity.

As an example, if $w = 10$ and $s = 11$, equation 1 tells us that $$ \sin(u)/u = 10/11; $$ From this, I conclude that $u \approx 0.748$ radians. And using the equality (in the middle of equation 1) that $\sin(u) = w/2r$, I get that \begin{align} r &= \frac{w}{2\sin u}\\ &= \frac{5}{\sin u}\\ &\approx \frac{5}{0.68}\\ &\approx 7.35\\ \end{align} Now equation 2 tells us that \begin{align} h &= \left( 4r^2 \sin^2(u/2) - \frac{w^2}{4} \right)^{\frac12}\\ &\approx \left( 4(7.35)^2 (.365)^2 - \frac{100}{4} \right)^{\frac12}\\ &\approx \left( 3.789 \right)^{\frac12}\\ &\approx 1.95 \end{align}

I know it's frustrating that finding the angle $u$ involves the inverse-sinc function, but sometimes that's how math works out.

John Hughes
  • 100,827
  • 4
  • 86
  • 159
  • 1
    Perhaps easier to write $h=\dfrac{w}{2} \dfrac{(1-\cos(u))}{\sin(u)}$ – Henry Jan 13 '25 at 14:39
  • 1
    No kidding! I didn't see that, so I went with the one I derived. Looks as if similar triangles are the secret sauce here. The nasty part is in finding $u$, alas. – John Hughes Jan 13 '25 at 14:43
  • $u \approx \sqrt{10-\sqrt{120 \frac{w}{a}-20}}$ is not bad and no doubt could be improved – Henry Jan 13 '25 at 15:25
  • Wow. Thanks. If you are interested, the OP asked this question which I answered but my trig was not sufficient to find a solid answer. I "left it as an exercise to the student" but the OP figured it was easier to ask here. – user1683793 Jan 15 '25 at 03:07
  • Thanks for the back-pointer. BTW, one answer to your question there about the rest of the structure expanding: If the steel beam has its ends held in place by a very strong concrete structure, for instance, the containing structure may not expand. This is, I believe, why many bridges have "expansion joints" to prevent bucking. – John Hughes Jan 15 '25 at 11:00