Usually when we refer to a vector in the context of games programming we mean a "geometric vector". If you really want to understand vectors in their totality eventually you'll need to learn about abstract vector spaces. These are pretty simple, but not so helpful when you're just learning!
I'll stick to calling "geometric vectors" just vectors. A vector has scalar components that represent a direction and length. A vector does not describe position, and has no location. In games vectors are usually used to describe a geometric direction, but can also be used to represent change.
It is important to understand that the Euclidean Basis in 3D is a matrix that looks like this:
[ i 0 0 ]
[ 0 j 0 ]
[ 0 0 k ]
i, j and k are all equal to 1. The Euclidean Basis is the identity matrix. The first column of this matrix represents the x axis. The second column represents the y axis. The third column represents the z axis. This matrix is just a group of three column vectors. Each column is called a basis vector.
A 3D vector has three scalar values and looks like this:
[ x y z ]
What do these three values x, y and z mean? These values represent how far along in the i, j and k directions the vector is composed of. So in reality when we write a 3D vector with x, y and z components, it is a short-hand notation of the following:
[ x * i, y * j, z * k ]
Now remember that i, j and k are column vectors! The above vector can also be written like this:
[ i ] [ 0 ] [ 0 ]
x * [ 0 ] + y * [ j ] + z * [ 0 ]
[ 0 ] [ 0 ] [ k ]
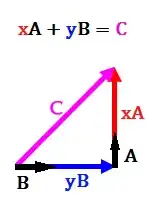
Above, all three column vectors of the Euclidean Basis are being scaled by the components of our 3D vector. This is called a linear combination. Any vector in 3D can be represented by a linear combination of the 3 basis vectors. The above is also the exact computation of multiplying a vector with a matrix! When we write our vectors down we're actually doing short-hand notation of matrix multiplication with the Euclidean Basis.
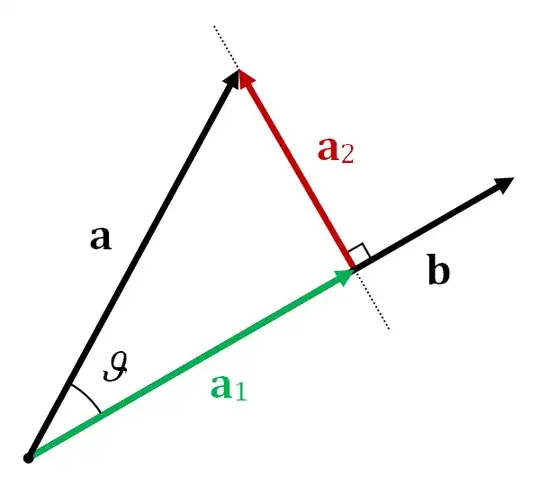
So when we project vector a onto vector b, we can see how for along the i, j and k directions b travels. We can also check out how far along a travels too. The difference between all of the directions from a and from b can be used to project one vector onto another.
If we want to project a onto b we can subtract away all of a that does not travel in the same direction as b. All that needs to be done is to calculate how far along in the b direction a goes. This last sentence is computed by the dot product.
I recommend reading the book Essential Mathematics by Jim Van Verth to learn all the important math concepts for game programming.