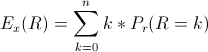Question on the 'Hat check' problem

Question

The famous 'Hat Check Problem' goes like this, 'n' men enter the restaurant and put their hats at the reception. Each man gets a random hat back when going back after having dinner. The goal is to find the expected number of men who get their right hat back. To calculate the expected value from is definition, we have to compute the probability with which 'k' men would get their correct hat back.

How to compute this probablity? I know that this problem can be solved by using 'Linearity of Expectation' in a much simpler way, but i would like to know the way to compute this probablity.

Answer 1

This is an arch-typical example where expectation is much easier than distribution...

There are $n$ hats and each person picks a hat uniformly at random hence each gets their right hat back with probability $\frac1n$. Expectation is linear even when the random variables are dependent hence the mean of the total number of persons who get their right hat back is $n\times\frac1n=1$.

Answer 2

Note that the combinatorial species $\mathcal{Q}$ of permutations with fixed points marked is $$\mathcal{Q} = \mathfrak{P} \left(\mathcal{U}\mathcal{Z} + \mathfrak{C}_2(\mathcal{Z}) + \mathfrak{C}_3(\mathcal{Z}) + \mathfrak{C}_4(\mathcal{Z})+\ldots\right).$$ Hence the generating function of these marked permutations is $$G(z, u) = \exp\left(uz+\frac{z^2}{2}+\frac{z^3}{3}+\frac{z^4}{4}+\ldots\right)$$ which is $$\exp\left(uz-z+\frac{z}{1}+\frac{z^2}{2}+\frac{z^3}{3}+\frac{z^4}{4}+\ldots\right) \\= \exp(uz-z) \exp\log\frac{1}{1-z} = \frac{1}{1-z} \exp(uz-z).$$

We can recover the total number of permutations on $n$ with $k$ fixed points from this generating function, it is given by $$n! [z^n][u^k]\frac{1}{1-z} \exp(uz-z) = n! [z^n] \frac{1}{1-z} \exp(-z) \frac{z^k}{k!} \\= \frac{n!}{k!} [z^{n-k}] \frac{1}{1-z} \exp(-z) = \frac{n!}{k!} \sum_{m=0}^{n-k}\frac{(-1)^m}{m!}.$$

It follows that the OGF of the expected number of fixed points is $$\left.\frac{d}{du} G(z,u)\right|_{u=1} = \left.\frac{1}{1-z} \exp(uz-z)\times z\right|_{u=1} = \frac{z}{1-z}. $$ Now since $$[z^n]\frac{z}{1-z} =1,$$ we expect there to be on average one person who recovers his hat.

The differentiation works here because it turns the term $q\times u^k \times z^n/n!$ into $q\times k\times z^n/n!$ and we see that the factor $n!$ which is necessary for the average is already present in the GF.

Answer 3

Hint: Use the principle of derangement (!n).

This is a classical problem and the below pdf gives the exact solution that you are looking for

Section 5 of the document gives you the answer. http://homepages.math.uic.edu/~kauffman/OldHats.pdf

Thanks

Satish

Answer 4

For each $S\in [n]$ such that $|S|=k$, let $f(S)$ be the number of elements $\pi \in \mathfrak {S}_{n}$ whose set of fixed points is exactly $S$: $$ f(S) = |\{\pi \in \mathfrak{S}_{n}: \pi(i)=i ~\text{iff}~~ i\in S\}| $$ Let $g(S)$ be the number of $\pi \in \mathfrak{S}_{n}$ whose set of fixed points includes $S$: $$ g(S) = |\{\pi \in \mathfrak{S}_{n}: \pi(i)=i ~~ \forall i\in S\}| $$ Clearly, $g(S)=\sum_{S \subseteq T\subseteq [n]} f(T)$. Mobius inversion gives \begin{align*} f(S) &= \sum_{S\subseteq T}(-1)^{|T\backslash S|}g(T)\\ &= \sum_{S\subseteq T} (-1)^{|T|-k} (n-|T|)!\\ &= \sum_{i=k}^{n} \sum_{|T|=i} (-1)^{i-k} (n-i)!\\ &= \sum_{i=k}^{n} \binom{n-k}{i-k} (-1)^{i-k}(n-i)!\\ &=(n-k)! \sum_{i=k}^{n} \frac{(-1)^{i-k}}{(i-k)!} \end{align*} Since there are $\binom{n}{k}$ ways to choose $S$, the total number of permutations in $\mathfrak{S}_{n}$ with $k$ fixed points equals $$ \binom{n}{k} \cdot (n-k)! \sum_{i=k}^{n} \frac{(-1)^{i-k}}{(i-k)!} = \frac{n!}{k!} \sum_{i=k}^{n} \frac{(-1)^{i-k}}{(i-k)!} $$