0

Consider a 3x3 chessboard with 9 elements. The elements are colored with black and white paints.

The task is to find the number of different chessboards of this type exist.

I don't know how to start with this problem....

user108696
  • 1
  • 1
    Does the orientation of the board matter? For instance, is the coloring that has a black square in the upper left corner and all the others squares white to be counted as different from the coloring that has a black square in the lower left corner and all the other squares white? Or are they to be counted as just one coloring, because the board can be rotated to turn one into the other? – Brian M. Scott Dec 13 '13 at 23:12
  • Draw a shape! And try to color it. Check if anything is ambiguous for you in the problem statement. – hhsaffar Dec 13 '13 at 23:12
  • This MSE link shows a solution that takes symmetries into account. – Marko Riedel Dec 13 '13 at 23:15
  • HINT: If the orientation of the board does matter, you’re really just counting the number of ways of choosing a subset of the $9$ elements to be colored black. How many subsets are there? – Brian M. Scott Dec 13 '13 at 23:20

2 Answers2

2

Suppose that rotating them does not matter, then we have two colors for each square and so a total of $2^9$ possibillities. For the other case, (possibillities that can be made by rotation of another possibillity are considered the same) we can use group theory. I will asume here that the bottom of the board is just black. Because we have $4$ possible roations and no mirroring (because the bottom of the board is black) we get as symmetry group $C_4$, the cyclic group of order $4$. No we will check the orbis of the squares after rotations. This will give us the following: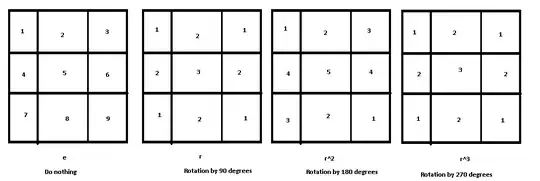enter image description here

So for the total possibillities we get (by The Counting Theorem): $$ \frac{1}{|G|}\sum_{g\in G} |X^g| = \\ \frac{1}{|C_4|} (1\cdot 2^9 + 4 \cdot 2^3 + 2 \cdot 2^5+ 4 \cdot 2^3)= \\ \frac{1}{4}(1\cdot 2^9 + 4 \cdot 2^3 + 2 \cdot 2^5+ 4 \cdot 2^3)= 160. $$ Where $X$ is the set of colourings of the chessboard and $X^g$ is the subset of $X$ consisting of those points which are left fixed by the element $g \in G$. So this will give us a total of $160$ chessboards, If the back of the chessboard is also in account, for example see-through, please add this to the question. This will give the symmetric group $D_4$ and some extra possobillities, for if you want to work it out.

user112167
  • 1,862
  • 1
    There should be no coefficients attached to the powers of $2$ in the above sum. The identity fixes $2^9$ boards, the rotations by $90^\circ$ and $270^\circ$ each fix $2^3$ boards, and the rotation by $180^\circ$ fixes $2^5$ boards. Thus, there are $(1/4)\cdot(2^9+2^3+2^3+2^5)=140$ different boards up to rotational symmetry. – Zack Cramer Dec 09 '19 at 22:08
1

If you consider rotations and reflections to be the same.

Number of $n\times n$ binary matrices under action of dihedral group of the square $D_4$.

http://oeis.org/A054247

$$a(n)=\begin{cases}\dfrac{1}{8}\left(2^{n^2}+2\cdot2^{n^2/4}+3\cdot2^{n^2/2}+2\cdot2^{(n^2+n)/2}\right) & n= 0\pmod2 \\ \dfrac{1}{8}\left(2^{n^2}+2\cdot2^{(n^2+3)/4}+2^{(n^2+1)/2}+4\cdot2^{(n^2+n)/2}\right)& n= 1\pmod2\end{cases}$$ \begin{align*} a(3)&=\,\dfrac{1}{8}\left(2^{3^2}+2\cdot2^{(3^2+3)/4}+2^{(3^2+1)/2}+4\cdot2^{(3^2+3)/2}\right)\\ &=\,\dfrac{1}{8}\left(2^{9}+2\cdot2^3+2^5+4\cdot2^6\right)=\dfrac{2^9+2^4+2^5+2^8}{8}=\,\quad{\large\color{red}{102}} \end{align*}

D.Matthew
  • 1,067