Suppose we want to count the number of non-decreasing sequences of $n$ non-negative integers which sum to $m$. That is, $a_{k+1}\ge a_k$ and
$$
\sum_{k=1}^na_k=m\tag{1}
$$
Note that if we set $a_0=0$, then
$$
\begin{align}
m
&=\sum_{k=1}^na_k\\
&=\sum_{k=1}^n\sum_{j=1}^k(a_j-a_{j-1})\\
&=\sum_{j=1}^n\sum_{k=j}^n(a_j-a_{j-1})\\
&=\sum_{j=1}^n(n-j+1)(a_j-a_{j-1})\tag{2}
\end{align}
$$
The following diagram illustrates $(2)$ for $n=4$:
$\hspace{4.5cm}$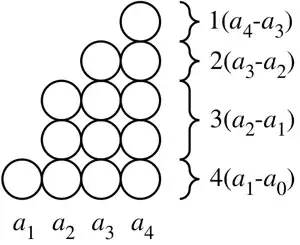
Consider the product
$$
\overbrace{(1+x^n+x^{2n}+\dots)}^{\large x^{(a_1-a_0)n}}
\overbrace{(1+x^{n-1}+x^{2(n-1)}+\dots)}^{\large x^{(a_2-a_1)(n-1)}}
\dots\overbrace{(1+x+x^2+\dots)}^{\large x^{a_n-a_{n-1}}}\tag{3}
$$
In the first factor, we choose $x^{(a_1-a_0)n}$. In the second factor, we choose $x^{(a_2-a_1)(n-1)}$. In the $k^\text{th}$ factor, we choose $x^{(a_k-a_{k-1})(n-k+1)}$. In the product, the coefficient of $x^m$ is the number of ways to make the sum in $(2)$.
The product in $(3)$ can be rewritten as
$$
\prod_{k=1}^n\frac1{1-x^k}\tag{4}
$$
The coefficient of $x^m$ in $(4)$ is the number of non-decreasing sequences of $n$ non-negative integers which sum to $m$.
The number of non-decreasing sequences of $n$ positive integers that sum to $m$ is the number of non-decreasing sequences of $n$ non-negative integers that sum to $m-n$. Just add $1$ to each element of the latter to get the former.
The number of increasing sequences of $n$ positive integers that sum to $m$ is the number of non-decreasing sequences of $n$ non-negative integers that sum to $m-n(n+1)/2$. Just add $k$ to the $k^\text{th}$ element of the latter to get the former.
The number of increasing sequences of $n$ non-negative integers that sum to $m$ is the number of non-decreasing sequences of $n$ non-negative integers that sum to $m-n(n-1)/2$. Just add $k-1$ to the $k^\text{th}$ element of the latter to get the former.
The number of non-decreasing sequences of $3$ positive integers that sum to $2010$ is the coefficient of $x^{2007}$ in
$$
\prod_{k=1}^3\frac1{1-x^k}\tag{5}
$$
which is $336675$. This matches the answer you give.
The number of increasing sequences of $3$ positive integers that sum to $203$ is the coefficient of $x^{197}$ in $(5)$, which is $3333$. This matches the official solution. However, the question asks for the number of non-decreasing sequences of $3$ positive integers that sum to $203$, which is the coefficient of $x^{200}$ in $(5)$, $3434$.
Closed Form for $(5)$
Since $(5)$ is the inverse of
$$
(1-x)(1-x^2)(1-x^3)=1-x-x^2+x^4+x^5-x^6\tag{6}
$$
the coefficients of $(5)$ are determined by
$$
a_n=a_{n-1}+a_{n-2}-a_{n-4}-a_{n-5}+a_{n-6}\\
(a_0,a_1,a_2,a_3,a_4,a_5,\dots)=(1,1,2,3,4,5,\dots)\tag{7}
$$
Since the roots of $(6)$ are $\left\{1,1,1,-1,e^{2\pi i/3},e^{-2\pi i/3}\right\}$, the solution of $(7)$ looks like
$$
a_n=c_0+c_1n+c_2n^2+c_3(-1)^n+c_4\cos(2\pi n/3)+c_5\sin(2\pi n/3)\tag{8}
$$
Using the initial values from $(7)$, we can compute the coefficients in $(8)$:
$$
a_n=\frac1{72}\left(47+36n+6n^2+9(-1)^n+16\cos(2\pi n/3)\right)\tag{9}
$$
Note that $9(-1)^n+16\cos(2\pi n/3)$ repeats mod $6$: $(25,-17,1,7,1,-17)$. Putting this together with $(9)$ yields
$$
a_n=\left\lfloor\frac{12+6n+n^2}{12}\right\rfloor\tag{10}
$$
Using $(10)$, we get $a_{2007}=336675$, $a_{197}=3333$, and $a_{200}=3434$, just as above.
