How many unique triangles are there with integer degree angles?
Like 60:60:60 is the equilateral. That's one. 1:2:177 is another. But not 2:1:177 because it is not a unique set of angles from a previous one. How many are there in total without repetitions?
I believe I have a correct answer. When I saw a pattern when writing them out manually and then assumed the pattern count was constant throughout. The number just "looks" correct, but I could be wrong.
What I want is a general concept of the combination problem and a formula that computes a correct answer of combinations for inputs of 180 and 3 (number of degrees and angles).
What combination formula applies to this question?
And what is the true count of unique triangles of integer degree angles?
=== New Addition below ===
I am looking for a formula and the logic behind it. A response like this: "the first angle can be 0 to 180 and the 2nd angle will be this minus 180 and the 3rd angle will be fixed by the other two. So the solution is 2 pick 180 minus some condition... which has this formula Y = Bla+Bla. And it is based on such and such combinatorial formula with this special condition for limiting shoices"
I already solved this through force using this logic:
0:0:180
0:1:179
0:2:178
0:3:177
...
0:89:91
0:90:90 = 91
1:1:178
1:2:176
...
1:89:90 = 89
2:2:176
...
2:87:91
2:88:90
2:89:89 = 88
3:3:174
3:4:173
...
3:87:90
3:88:89 = 86
...
4:4:172
4:5:171
...
4:87:89
4:88:88 = 85
5:5:170
...
5:87:88 = 83
6:6:168
...
6:87:87 = 82
7:7:166
...
7:86:87 = 80
8:8:164
...
8:86:86 = 79
9:9:162
...
9:85:86 = 77
......
56:56:68
56:57:67
56:58:66
56:59:65
56:60:64
56:61:63
56:62:62 = 7
57:57:66
57:58:65
57:59:64
57:60:63
57:61:62 = 5
58:58:64
58:59:63
58:60:62
58:61:61 = 4
59:59:62
59:60:61 = 2
60:60:60 = 1
= 1+2+4+5+7+8+ ... +86+88+89
= 1+2+3+4+ ... +89 - (3+6+9+...+87)
= 1+2+3+4+ ... +89 - 3*(1+2+3+ ... +29)
= (90)(90)/2 - 3(30)(30)/2
= (90^2-330^2)/2
= 2700
- now 2700 seems like a large number, but it seems correct according to its relation with 360.
But I could be wrong and I suspect knowledge of a formula would make it faster and easier for me next time.
=== This image helped me understand why it is 2700. The image is the graph of two angles of a triangle. Axis are the first and second angle. The graph triangle is base 180, height 180 and has area = $180×180/2 = 180^2/2$. There are 6 reflected images in the graph. So divide by 6 to get the answer $180^2/12 = 2700$.
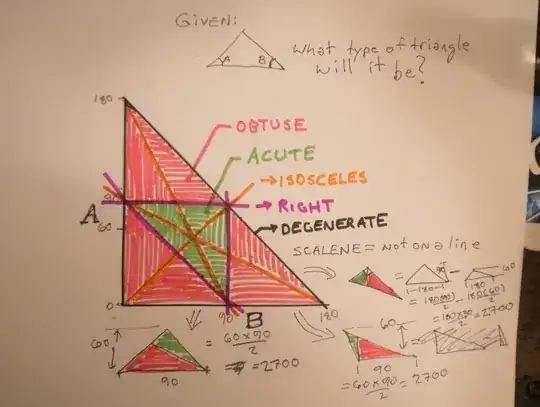
The third angle is irreverent since it is fixed by the selection of the first two. That would provide 180 * 180 choices = 180^2. But the Second angle cannot be greater than the first so that removes half to selections leaving 180^2/2 selections. But for any 3 angle choices there are 6 rearrangements. So we divide by 6 leaving: 180^2/12 = 2700.
– peawormsworth Jul 09 '21 at 07:35