Motivation :
I want to make a simpler version of Yu, K.: $p$-adic logarithmic forms and group varieties for $\alpha_i,b_i \in \mathbb{Z}$,
to solve problems like this one : Let $n$ a positive integer , show that $2^{n+3} \mid 3^n +7$ has no solutions? or : $3^n$ does not divide $4^n+5$ for $n\geq 2$ , A Conjecture about the upper bound of $v_2(3^n+d)$
some basic notations :
$v_p(x)$ is the $p$-adic valuation of $x$
$\log(x)$ is referred to it in this article as $\ln(x)$
My attempt :
In the reference, $d$ is defined as $d=[K:\mathbb{Q}]$, where $K=\mathbb{Q}(\alpha_1,...,\alpha_n)$.
This is the degree of the number field, since $\alpha_i \in \mathbb{Z} \Rightarrow d=1$
- the ramification index $e_{\mathfrak{p}}$ is the exponent of $\mathfrak{p}$ in the factorization:
$$p O_K = \mathfrak{p}_1^{e_1} \mathfrak{p}_2^{e_2} \cdots \mathfrak{p}_g^{e_g}$$
In $\mathbb{Z}$, for any prime number $p \in \mathbb{Z}$, the ideal $p\mathbb{Z}$ factors as:
$$p\mathbb{Z} = (p)^1$$
where $(p)$ is a prime ideal in $\mathbb{Z}$ $\Rightarrow$ The ramification index $e_\mathfrak{p} = 1$
- the residue class degree $f_\mathfrak{p}$ is:
$$f_\mathfrak{p} = [O_K/\mathfrak{p} : \mathbb{Z}/p\mathbb{Z}]$$
In $\mathbb{Z}$ (where $O_K = \mathbb{Z}$ and $\mathfrak{p} = p\mathbb{Z}$), this becomes:
$$f_\mathfrak{p} = [\mathbb{Z}/p\mathbb{Z} : \mathbb{Z}/p\mathbb{Z}] = 1$$
- $h_i=\max(h_0(\alpha_i),\log(p))$, ($1 \le i \le n$) where $h_0$ is the absolute logarithmic Weil height
Let $\alpha \neq 0$ be an algebraic number and $$m_\alpha(x) = a_0x^d + a_1x^{d-1} + \cdots + a_{d-1}x + a_d$$ its minimal polynomial in $\mathbb{Z}[x]$. The Weil height of $\alpha$ is given by $$h(\alpha) = d^{-1} \int_0^1 \log \left| m_\alpha \left( e^{2\pi i t} \right) \right| dt.$$
Again, as $\alpha_i \in \mathbb{Z}$, we can take $h_0(\alpha_i)=\log(\left| \alpha_i \right|) \Rightarrow h_i=\log(\max(\left| \alpha_i \right|,p))$
- $B$ be a real number satisfying $B \ge \max(\left|b_1\right|, ... , \left|b_n\right|, 3)$
For simplicity, we will take $B=\max(\left|b_1\right|, ... , \left|b_n\right|, 3)$
the result from Kunrui Yu gives that : $$ v_p(\alpha_1^{b_1} \cdots \alpha_n^{b_n} - 1) < 19(20\sqrt{n+1}\cdot d)^{2(n+1)} e_{\frak{p}}^{n-1} \frac{p^{f_{\frak{p}}}}{(f_{\frak{p}} \log(p))^2} \log(e^5 n d) h_1 \cdots h_n \log(B). $$
for $\alpha_i$ integers, $d=e_\mathfrak{p}=f_\mathfrak{p}=1$ :
$$ v_p(\alpha_1^{b_1} \cdots \alpha_n^{b_n} - 1) < 19(20\sqrt{n+1})^{2(n+1)} \frac{p}{\log(p)^2} (5 + \log(n)) h_1 \cdots h_n \log(B). $$
if $n$ is fixed in $\mathbb{N^*}$ and our $\alpha_i$ are fixed in $\mathbb{Z}$:
$$ v_p(\alpha_1^{b_1} \cdots \alpha_n^{b_n} - 1) < C_n \log(B) \Rightarrow v_p(\alpha_1^{b_1} \cdots \alpha_n^{b_n} - 1) = \mathcal{O}(\log(B)) $$
where $C_n$ is an enormous big constant !
$\Rightarrow \exists b_0, \forall B>b_0, v_p(\alpha_1^{b_1} \cdots \alpha_n^{b_n} - 1) < B$
Since the inequality $B<C_n \log(B)$, won't last longer !
My question :
how to reduce this enormous constant $C_n$ to something reasonable ?
Example : Let $n$ a positive integer , show that $2^{n+3} \mid 3^n +7$ has no solutions?
$n=p=2, \alpha_1 = 3, b_1=t , \alpha_2=-7 , b_2=-1$
$\Rightarrow v_2(3^t \cdot (-7)^{-1}-1) < C_2 \log(B)$ , where $B=\max(\left|b_1\right|, ... , \left|b_n\right|, 3)$
Assuming $t\ge3 \Rightarrow B=t \Rightarrow v_2(3^t + 7) < C_2 \log(t) $
To compute $h_1,h_2$ we will use our nice formula $h_i=\log(\max(\left| \alpha_i \right|,p))$
$\Rightarrow h_1=\log(\max(\left| 3 \right|,2))=\log(3) , h_2=\log(\max(\left| -7 \right|,2))=\log(7) $
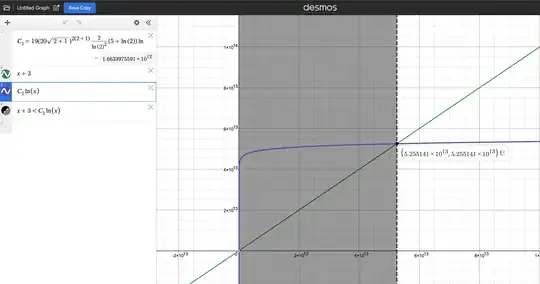
$\Rightarrow C_2=19(20\sqrt{2+1})^{2(2+1)} \displaystyle\frac{2}{\log(2)^2} (5 + \log(2)) \log(3) \log(7) \approx 1.6633975591\times10^{12} < 1.6634 \times10^{12} $
$\Rightarrow v_2(3^t + 7) < 1.6634 \times10^{12} \log(t)$
Thus, for a solution to $2^{t+3} \mid 3^t +7$ we have to have :
$t+3<1.6634 \times10^{12} \log(t) \Rightarrow t < 5.255141\times10^{13}$ a (quite inpractical) upper bound !
Calculations were done here here in Desmos !
[$1$]: Yu, K.: p-adic logarithmic forms and group varieties. II. Acta Arith. $89(4)$, $337–378$ $(1999)$, https://bibliotekanauki.pl/articles/1390501.pdf
Thanks for help !