4

The conjecture :

$\forall n>1, d\mid 3^n-2^n \Rightarrow v_2(d+1)<n$

where $v_2(x)$ denotes the $2$-adic valuation of $x$, i.e the highest power of $2$ that divides $x$

e.g : $v_2(12)=2$ since $12=2^2 \cdot 3$

Initially, let's check the case when $d=3^n-2^n$

$\Rightarrow v_2(d+1)=v_2(3^n+1-2^n)$

Notice that, $v_2(3^n+1)=\begin{cases} 1 \text{ , if } n \equiv 0 \pmod 2 \\ \\ 2 \text{ , if } n \equiv 1 \pmod 2 \end{cases}$

$\Rightarrow v_2(d+1) =\begin{cases} v_2(2^1\times(\displaystyle \frac{3^n+1}{2}-2^{n-1})) = 1 \text{ , if } n \equiv 0 \pmod 2 \\ \\ v_2(2^2\times(\displaystyle \frac{3^n+1}{2^2}-2^{n-2}))=2 \text{ , if } n \equiv 1 \pmod 2 \end{cases} $

You can take $n>2 \Rightarrow v_2(d+1) < n$, the case $n=2$ is correct since $2$ is even and $2>1$

Also, the case $d=1$ is trivial since $v_2(d+1)=v_2(1+1)=1<2<n$

  • @Aphelli noticed that $d\mid 3^n-2^n \Leftrightarrow \displaystyle \left(\frac{3}{2}\right)^n \equiv 1 \pmod d $

So it's enough to prove the following :

$\gcd(d,6)=1 \Rightarrow v_2(d+1) < \text{ord}_d \displaystyle \left(\frac{3}{2}\right)$

My attempt :

Firstly, we clearly notice that $d\mid 3^n-2^n \Rightarrow d$ is odd $ \Rightarrow 2\mid d+1$

Let's assume by contradiction, that $v_2(d+1)\ge n \Rightarrow 2^n \mid d+1 \Rightarrow d=2^nk-1$

$\Rightarrow 2^nk-1 \mid3^n-2^n$ , (for some integer $k \ge 1$)

e.g : for $k=1 \Rightarrow 2^n -1 \mid 3^n-2^n=3^n-(2^n-1)-1$

$\Rightarrow 2^n-1 \mid 3^n-1 \Rightarrow n$ is odd , (since $2\mid n \Rightarrow 3\mid 3^n-1$)

Let's use the Jacobi symbol :

$\displaystyle \left( \frac{3}{2^n-1} \right)=1 \Rightarrow \displaystyle \left( \frac{2^n-1}{3} \right) = (-1)^{\displaystyle\frac{3-1}{2} \times \frac{2^n-1-1}{2}}=-1$

On the other hand, $2^n-1\equiv (-1)^n-1 \equiv -2 \equiv 1 \pmod 3$

$\Rightarrow \displaystyle \left( \frac{2^n-1}{3} \right) = \displaystyle \left( \frac{1}{3} \right) = +1$ , which is a contradiction !

we conclude the following :

Fix $k \in \mathbb{N^*} \implies 2^nk-1 \mid3^n-2^n$ has only finite solutions for $n>1$

$2^nk-1 \mid3^n-2^n \Rightarrow (2^nk-1)\lambda = 3^n-2^n$ , (for some integer $\lambda \ge 1$)

$\Rightarrow 2^n(\lambda k +1)=3^n+\lambda \Rightarrow v_2(3^n+\lambda) \ge n$

which won't last longer, since $\forall d \in \mathbb{N^*}, \exists n_0 \in \mathbb{N^*}$ such that : $\forall n>n_0 : v_2(3^n+d)<n$ , where $n$ is a positive integer.

Also, if someone managed to optimize the constant $C_n$ mentioned on : Analyzing Yu, K.: $p$-adic logarithmic forms and group varieties

we may deduce some tighter bounds on $n$ or $\lambda$, which would contradict the fact that $\lambda < 3^n - 2^n$

I've also checked the conjecture $\forall n<10^2$, by python :

from sympy import divisors

def val_2(n):
    return (n & -n).bit_length() - 1


for n in range(2,pow(10,2)):
    for d in divisors(pow(3,n)-pow(2,n)):
        if val_2(d+1) >= n :
            print(f'Contradiction at n={n} , d={d}')
            break

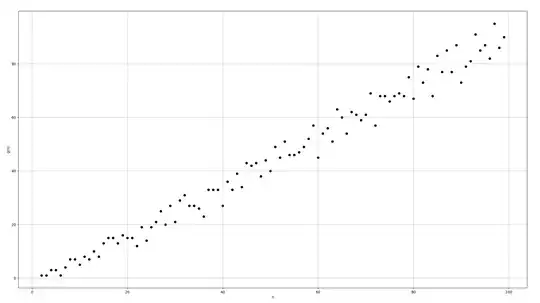
Also, setting $G_n$ to be the set of gaps $n-v_2(d+1) , \forall d\mid 3^n-2^n $ and $g(n)=\min(G_n)$

we remark that $g(n) > 0$ and $g(n)=\mathcal{O}(n)$

g(n) in function of n

So, as $n$ grows up $v_2(d+1)$ became much smaller than $n$ which is assured by our conjecture !

from sympy import divisors
import matplotlib.pyplot as plt

def val_2(n):
    return (n & -n).bit_length() - 1


plt.grid(True)
plt.xlabel("n")
plt.ylabel("g(n)")
for n in range(2,pow(10,2)):
    G=[]
    for d in divisors(pow(3,n)-pow(2,n)):
        G.append(n-val_2(d+1))
    plt.scatter(n,min(G),c='black')


plt.show()

Thanks for help !

Lhachimi
  • 105

0 Answers0