On the behaviour of a function around branch cuts

Question

I'm a physics student. I'm currently taking a complex analysis course and I'm struggling to understand how the determination of a function is given on its branch cut. Since it is hard for me to even formulate what I don't understand, I will try to lay out my reasoning using an exercise I was given, and asking questions along. I have this integral:

$$ I = \int_0^{+\infty} \frac{dx}{\sqrt[3]{x} (x + 1)} $$

Now I can bind the integral over the real number field to one on the complex field, considering the complex function:

$$f(z) = \frac{1}{\sqrt[3]{z} (z+1)}$$

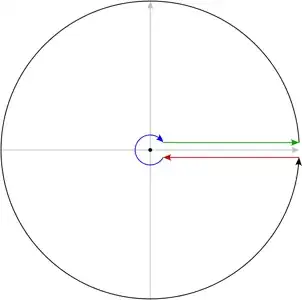
As I've understood, since $\sqrt[3]{z}$ has a branch point in $z_0 = 0$ (and $z_1 = \infty$) it is necessary to place a branch cut on the complex plane. Here it is the first question. Can I place the branch cut wherever I want, as long as it connects the two singular $z_0$ and $z_1$? Up until now, I assumed I can. I choose to place the branch cut on the real axis in $[0, +\infty]$. The integration contour is the following:

I will refer to the whole curve as $\Gamma$, to the black arc as $\phi_R: z = Re^{i\theta}$ and to the blue part as $\gamma_\epsilon: z = \epsilon e^{i\theta}$:

$$ \oint_\Gamma f(z)dz = \int_{\phi_R} f(z)dz + \int_R^\epsilon f(z)dz + \int_{\gamma_\epsilon} f(z)dz + \int_\epsilon^R f(z) dz$$

Now, I can take a limit:

$$ \lim_{\begin{aligned} R &\to +\infty \\ \epsilon &\to 0 \end{aligned}}\oint_\Gamma f(z)dz = \lim_{R \to +\infty} \int_{\phi_R} f(z)dz + \lim_{\epsilon \to 0} + \int_{\gamma_\epsilon} f(z)dz + \lim_{\begin{aligned} R &\to +\infty \\ \epsilon &\to 0 \end{aligned}} \left(\int_R^\epsilon f(z)dz + \int_\epsilon^R f(z)dz \right) $$

$$ \lim_{\begin{aligned} R &\to +\infty \\ \epsilon &\to 0 \end{aligned}}\oint_\Gamma f(z)dz = \int_{+\infty}^0 f(x^+)dx + \int_0^{+\infty} f(x^-)dx = \int_0^{+\infty} (-f(x^+) + f(x^-)) dx = 2 \pi i \sum_{i \: s.t. \: z_i \in \mathring{\Gamma}} \mathrm{Res}[f(z), z_i]$$

where, with $f(x^+)$ and $f(x^-)$ I am referring to the value of the function over and below the cut of the function. It is necessary to determine the form of the function over and under the cut.

Now the core of my question. How do I provide the determination of the function? The thing is that I cannot figure out what comes first and what follows when one has to provide the determination of the function. Now as I understand I need to choose a Riemann sheet to calcuate the integral on. What does it specifically mean to choose on a specific Riemann sheet? Now I thought that the function over and under the branch cut has two different forms, because when crossing the cut one also change Riemann sheet. However sometimes it seems as if, in the example exercises, two forms of the function are given, one over and one under the cut. I've come up with two different procedures to try to give some motivation to example exercises:

reasoning 1) $$ \sqrt[3]{z} = \left( \rho e^{i\left( \theta + 2k \pi \right)} \right)^{\frac{1}{3}} = \sqrt[3]{\rho} e^{i \left( \frac{\theta}{3} + \frac{2}{3} k \pi \right)} = \begin{cases} \sqrt[3]{\rho} e^{i \frac{\theta}{3}} &\longrightarrow \textbf{first form} \\ \sqrt[3]{\rho} e^{i(\frac{\theta}{3} + \frac{2}{3}\pi)} &\longrightarrow \textbf{second form} \\ \sqrt[3]{\rho} e^{i(\frac{\theta}{3} + \frac{4}{3}\pi)} &\longrightarrow \textbf{third form} \end{cases}$$

\begin{align} z = x^+ && 0 < x && \Longrightarrow && &\text{we are over the cut} && \Longrightarrow && \theta = 0 && \Longrightarrow && \begin{cases} \sqrt[3]{x} \\ \sqrt[3]{x} e^{\frac{2}{3}\pi i} \\ \sqrt[3]{x} e^{\frac{4}{3}\pi i}\end{cases} && \xrightarrow{\textbf{I choose the first form}} && \sqrt[3]{z} = \sqrt[3]{x}\\ z = x^- && 0 < x && \Longrightarrow && &\text{we are under the cut} && \Longrightarrow && \theta = 2\pi && \Longrightarrow && \begin{cases} \sqrt[3]{x} e^{\frac{2}{3}\pi i} \\ \sqrt[3]{x} e^{\frac{4}{3}\pi i} \\ \sqrt[3]{x} \end{cases} && \xrightarrow{\textbf{I choose the second form}} && \sqrt[3]{z} = \sqrt[3]{x} e^{\frac{4}{3} \pi i} \end{align}

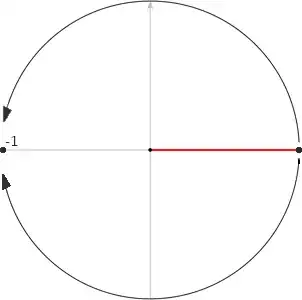
Note the implication arrow, as one of my core doubts is what comes first in the reasoning. Now the question related to this kind of reasoning: is it necessary to take the angle over and under the cut to be out of phase of $2 \pi$ or is it possible to choose both angle to be $0$ or $2\pi$? in fact, if I place a point on the cut, exactly on the cut, I cannot determine wheter I have approached the cut from over or under, therefore the only way of telling is using the phase, nevertheless, this kind of reasoning doesn't satisfy me. as, in other examples, I saw that, in order to determine the value of the function $\sqrt[3]{z}$ outside the cut, for instance in $-1$, one can take a path connecting a point on the cut to $z = -1$. If the path is taken to begin over the cut, then

$$ \theta^{(0)} = 0 \to \theta = \pi \xrightarrow[\text{as it is the one chosen over the cut}]{\text{plug it in into the first form}} \sqrt[3]{z} = \sqrt[3]{\rho} e^{i\frac{\theta}{3}} = \sqrt[3]{1} e^{i0} = 1$$

if the path is taken to begin under the cut, then

$$ \theta^{(0)} = 0 \to \theta = -\pi \xrightarrow[\text{as it is the one chosen under the cut}]{\text{plug it in into the second form}} \sqrt[3]{z} = \sqrt[3]{\rho} e^{i(\frac{\theta}{3} + \frac{2}{3}\pi)} = \sqrt[3]{1} e^{i\frac{\pi}{3}} = e^{i\frac{\pi}{3}}$$

How is it possible to for $\sqrt[3]{z}$ to have different values in $-1$ if it is monodrome everywhere but on the cut? Had have I followed the previous remark the question still holds: adding $2\pi$ to the phase with which one starts over the cut, the value in $-1$ continues to be different:

$$ \theta^{(0)} = 0 \to \theta = 2\pi \xrightarrow[\text{as it is the one chosen under the cut}]{\text{plug it in into the second form}} \sqrt[3]{z} = \sqrt[3]{\rho} e^{i(\frac{\theta}{3} + \frac{2}{3}\pi)} = \sqrt[3]{1} e^{i\frac{4}{3}\pi} = e^{i\frac{4\pi}{3}}$$

reasoning 2)

$$ \sqrt[3]{z} = \left( \rho e^{i\left( \theta + 2k \pi \right)} \right)^{\frac{1}{3}} = \sqrt[3]{\rho} e^{i \left( \frac{\theta}{3} + \frac{2}{3} k \pi \right)} = \begin{cases} \sqrt[3]{\rho} e^{i \frac{\theta}{3}} &\longrightarrow \textbf{first form} \\ \sqrt[3]{\rho} e^{i(\frac{\theta}{3} + \frac{2}{3}\pi)} &\longrightarrow \textbf{second form} \\ \sqrt[3]{\rho} e^{i(\frac{\theta}{3} + \frac{4}{3}\pi)} &\longrightarrow \textbf{third form} \end{cases}$$

I choose the first form $\sqrt[3]{z} = \sqrt[3]{\rho} e^{i\frac{\theta}{3}} \Longrightarrow$ \begin{align} z &= x^+ && 0 < x && \Longrightarrow && \text{over the cut} && \Longrightarrow && \theta = 0 && \Longrightarrow && \sqrt[3]{z} = \sqrt[3]{\rho} \\ z &= x^+ && 0 < x && \Longrightarrow && \text{under the cut} && \Longrightarrow && \theta = 2\pi && \Longrightarrow && \sqrt[3]{z} = \sqrt[3]{\rho} e^{\frac{2}{3} \pi i} \end{align}

Again, note the implication arrows. In this case the the phase over and under the cut must be out of phase of $2\pi$, I think, otherwise, the function would have the same form over and under the cut, which is not possible. The rest of the exercise is not important to me right now.

Summing up all the questions:

1. Can I place the branch cut wherever I want, as long as it connects the two singular points?
2. In general, what does it mean to choose a certain Riemann sheet?
3. How does the reasoning to provide the function form and determination over and under the cut work?
   1. do the angles over and under the cut need to be out of phase of a factor of $2 \pi$?
   2. do I choose two forms of the function or just one?
4. Why doesn't the function have the same value outside the cut when calculating it using different paths?

I've been trying to understand this for the most part of the course, but still reached no conclusion. So, thanks a lot in advance for your help!

Answer 1

You're aiming to recover the result of: $$v = \int_0^{+\infty} \frac{1}{\sqrt[3]{x} (x + 1)}dx$$ along the real numbers. The function doesn't have unique values on the complex plane, So you'll want your choice of Riemann sheet to give the correct values on the $[0,\infty)$ segment.

Ideally the branch cut should be defined along the segment you want to integrate. So, by taking the polar form of a complex number to be:

$$z = pe^{i\theta}$$

where: $\theta\in[0,2\pi)$ and $p \geq 0$, we may define $\sqrt[3]{z} = \sqrt[3]{p} \;e^{i\frac{\theta}{3}}$.

This gives us a single-valued function to work with. Our choice of interval $\theta\in[0,2\pi)$ determines the location of the branch cut and is vital in resolving ambiguities.

Our single-valued function can be stated as:

$$f(pe^{i\theta}) = \frac{1}{ (\sqrt[3]{p} \;e^{i\frac{\theta}{3}}) (pe^{i\theta} + 1)} $$

where $\theta\in[0,2\pi)$ and $p \geq 0$.

In order to successfully apply the residue theorem (whilst still working only in our single-valued branch), our closed path must not cross the cut. As it goes counter-clockwise along the simple pole at $z = -1$, the total integral has a value of: $$\lim_{z\rightarrow (-1)} 2\pi i (z+1)f(z) = 2\pi i \frac{1}{\sqrt[3]{1}\;e^{i\frac{\pi}{3}}} = 2\pi i \frac{1}{2}(1-i\sqrt{3})= \pi(\sqrt{3}+i)$$

The outer and inner circles of the path can be proven to go to $0$. We are interested in the sum of the integrals of the blue path and red path.

The points on the blue path take values of $f(p)$, while the "neighboring" points on the red path (across the cut) take values of $f(pe^{i \theta})$, where $\theta < 2\pi$, $ $ yet $\theta \rightarrow 2\pi$ in the limit. We may compute: $$\lim^{\theta < 2\pi}_{\theta\rightarrow 2\pi} f(p e^{\theta}) = \frac{f(p)} { e^{i\frac{2\pi}{3}}}$$

From this we get that in the limit, the integral along the red path is equal to $- (v / e^{i\frac{2\pi}{3}})$ where $v$ is the integral along the blue path. The minus sign is due to opposing directions. Putting it all together we get:

$$v - (v / e^{i\frac{2\pi}{3}}) = \pi(\sqrt{3}+i)$$ $$v = \frac{2\pi}{\sqrt{3}} $$

---

(1) Technically the cut can be placed anywhere as long as it connects the singularities, yet practically it shouldn't "cut" (create a discontinuity) in the path you're actually trying to integrate (in our case the interval $(0,\infty)$ along the real line).

(2 and 3) Just chose a definition for the function that gives at most one value at every point and is continuous everywhere except the cut. Make sure it matches the intended values along the path you want to integrate.

(4) It should have exactly the same values unless the paths "cross the cut". In our example for the points $p\in(0,\infty)$ were assigned exactly one value which was matched if we took limit points from the upper complex half-plane. Yet if we took limit points from the lower complex half-plane we obtained "shifted" values. The blue part of the integral was defined as laying in $p\in(0,\infty)$, the red part was defined as laying below. We take the limit of a set of paths where the red part approaches the real line from below, so the computation worked out.

You can technically say that in the limit the red part is in $p\in(0,\infty)$ taking different values than the blue part (we're working again with the many-valued function, not the branch), but this would complicate things.