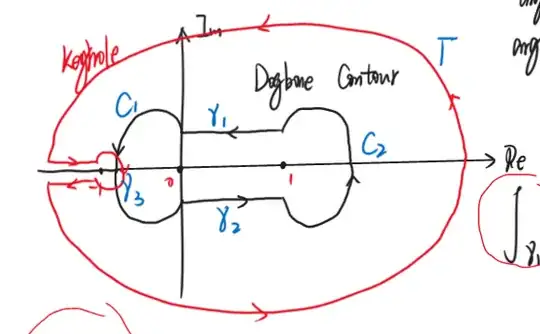
This first part of my answer is me expanding on my comment. TLDR: the mistake is within your residue calculation. Using the formula for Residues at Mulitple-Order Poles, we get
$$
\begin{align}
-\frac{2\pi i}{1+i}\mathop{\mathrm{Res}}_{z=-1}f(z) &= -\frac{2\pi i}{1+i}\left(\frac{1}{(3-1)!}\right)\lim_{z\to -1}\frac{d^{3-1}}{dz^{3-1}}(z-(-1))^3f(z) \\
&= -\frac{\pi i}{1+i} \lim_{z\to -1}\frac{d^{2}}{dz^{2}}z^{\frac{1}{4}}\left(1-z\right)^{\frac{3}{4}} \\
&= \frac{3\pi i}{16\left(1+i\right)}\lim_{z\to -1}z^{-\frac{7}{4}}\left(1-z\right)^{-\frac{5}{4}} \\
&= \frac{3\pi i}{16\left(1+i\right)}\lim_{z\to -1}\exp\left(-\frac{7}{4}\ln\left|z\right|-\frac{7i}{4}\arg z\right)\exp\left(-\frac{5}{4}\ln\left|1-z\right|-\frac{5i}{4}\arg\left(1-z\right)\right) \\
&= \frac{3\pi i}{16\left(1+i\right)}\exp\left(-\frac{7}{4}\ln\left(1\right)-\frac{7i}{4}\arg\left(-1\right)\right)\exp\left(-\frac{5}{4}\ln\left(2\right)-\frac{5i}{4}\arg\left(2\right)\right)\,. \\
\end{align}
$$
You defined $-\pi\le\arg z\le\pi$ and $0\le\arg\left(1-z\right)\le2\pi$. Including both endpoints of the intervals may seem like it is not that big of an issue. But to calculate $\arg(-1)$, it would equal both $-\pi$ and $\pi$. Same idea goes for calculating $\arg(2)$. Keeping functions single-valued in this situation is important.
Let's go with $-\pi<\arg z\le\pi$ and $0\le\arg\left(1-z\right)<2\pi$ for now and see what happens. The residue becomes
$$
\begin{align}
\frac{3\pi i}{16\left(1+i\right)}\exp\left(-\frac{7}{4}\ln\left(1\right)-\frac{7i}{4}\arg\left(-1\right)\right)\exp\left(-\frac{5}{4}\ln\left(2\right)-\frac{5i}{4}\arg\left(2\right)\right) &= \frac{3\pi i}{16\left(1+i\right)}\exp\left(-\frac{7i}{4}\cdot\pi\right)\exp\left(-\frac{5}{4}\ln\left(2\right)-\frac{5i}{4}\cdot0\right) \\
&= 3\pi i\cdot2^{-\frac{23}{4}}\,. \\
\end{align}
$$
This is where the extra $i$ factor comes from, which is obviously incorrect because the original integral equals a real number.
On the other hand, if we choose $-\pi<\arg z\le\pi$ and $0<\arg\left(1-z\right)\le2\pi$, then we get
$$
\begin{align}
\frac{3\pi i}{16\left(1+i\right)}\exp\left(-\frac{7}{4}\ln\left(1\right)-\frac{7i}{4}\arg\left(-1\right)\right)\exp\left(-\frac{5}{4}\ln\left(2\right)-\frac{5i}{4}\arg\left(2\right)\right) &= \frac{3\pi i}{16\left(1+i\right)}\exp\left(-\frac{7i}{4}\cdot\pi\right)\exp\left(-\frac{5}{4}\ln\left(2\right)-\frac{5i}{4}\cdot2\pi\right)\\
&= 3\pi\cdot2^{-\frac{23}{4}}\,.
\end{align}
$$
Side note... I suppose that you would need to experiment with choosing which endpoints of the intervals to include and to not include when doing the calculations, because it's not clear to me how someone can guess the correct intervals immediately without trial and error.
Finally, the YouTuber "qncubed3" has a solution to a similar problem you may find useful: Complex Analysis: Dogbone Contour Example #2.
For my enjoyment and hopefully yours, here is the full solution.
Let $\mathcal{I}$ be the integral in question. Define $f: \mathbb{C}\,\backslash ([0,1]\cup\left\{-1\right\}) \to \mathbb{C}$ where
$$z \mapsto \frac{\left|z\right|^{\frac{1}{4}}\left|1-z\right|^{\frac{3}{4}}\exp\left(\frac{i}{4}\arg z\right)\exp\left(\frac{3i}{4}\arg\left(1-z\right)\right)}{\left(1+z\right)^{3}}\,.$$
Here, we define $-\pi<\arg z\le\pi$ and $0<\arg\left(1-z\right)\le2\pi$. We exclude $[0,1]$ from the domain. This is because when the branch of $\arg z$ lies on $(\infty,0]$ and when the branch of $\arg(1-z)$ lies on $(-\infty,1]$ (since the negative sign in front of the $z$ would "flip" the branch pointing right to the left instead), the branches "cancel out" on $(-\infty,0)$.
To prove they cancel out, we'll show that the numerator of $f$ is continuous on $(-\infty,0)$. Let $a>0$, let $\varepsilon > 0$, and $g(z)$ equal the numerator of $f(z)$. When we approach the negative real axis from above, we get
$$
\begin{align}
\lim_{\varepsilon\to0^+}g(-a+i\varepsilon)&=\lim_{\varepsilon\to0^+}\left|-a+i\varepsilon\right|^{\frac{1}{4}}\left|1-(-a+i\varepsilon)\right|^{\frac{3}{4}}\exp\left(\frac{i}{4}\arg (-a+i\varepsilon)\right)\exp\left(\frac{3i}{4}\arg\left(1-(-a+i\varepsilon)\right)\right) \\
&=\left|-a+i\cdot0\right|^{\frac{1}{4}}\left|1-\left(-a+i\cdot0\right)\right|^{\frac{3}{4}}\exp\left(\frac{i}{4}\cdot\pi\right)\exp\left(\frac{3i}{4}\cdot2\pi\right) \\
&= a^{\frac{1}{4}}\left(1+a\right)^{\frac{3}{4}}\exp\left(\frac{7\pi i}{4}\right)\,. \\
\end{align}
$$
When we approach the real axis from below, we get
$$
\begin{align}
\lim_{\varepsilon\to0^+}g(-a-i\varepsilon)&=\lim_{\varepsilon\to0^+}\left|-a-i\varepsilon\right|^{\frac{1}{4}}\left|1-(-a-i\varepsilon)\right|^{\frac{3}{4}}\exp\left(\frac{i}{4}\arg (-a-i\varepsilon)\right)\exp\left(\frac{3i}{4}\arg\left(1-(-a-i\varepsilon)\right)\right) \\
&=\left|-a-i\cdot0\right|^{\frac{1}{4}}\left|1-\left(-a-i\cdot0\right)\right|^{\frac{3}{4}}\exp\left(\frac{i}{4}\cdot(-\pi)\right)\exp\left(\frac{3i}{4}\cdot0\right) \\
&= a^{\frac{1}{4}}\left(1+a\right)^{\frac{3}{4}}\exp\left(-\frac{\pi i}{4}\right)\,.\\
\end{align}
$$
Since $\exp\left(\frac{7\pi i}{4}\right) = \exp\left(-\frac{\pi i}{4}\right)$, we have continuity across $(-\infty,0)$ for $g$.
Next, we construct a dogbone/dumbbell contour like your screenshot. Let $\mathcal{C}$ be the positively oriented contour comprised of the union of sets below:
$$
\begin{align}
\gamma_1 &:= \left\{-t+i\delta \in \mathbb{C} : t \in \left[\sqrt{r^{2}-\delta^{2}}-1, -\sqrt{r^{2}-\delta^{2}}\right]\right\}\\
C_1 &:= \left\{re^{it} \in \mathbb{C} : t \in \left[\arctan\left(\frac{\delta}{\sqrt{r^{2}-\delta^{2}}}\right), 2\pi-\arctan\left(\frac{\delta}{\sqrt{r^{2}-\delta^{2}}}\right)\right]\right\}\\
\gamma_2 &:= \left\{t-i\delta \in \mathbb{C} : t \in \left[\sqrt{r^{2}-\delta^{2}},1-\sqrt{r^{2}-\delta^{2}}\right]\right\}\\
C_2 &:= \left\{1+re^{it}: t \in \left[-\pi+\arctan\left(\frac{\delta}{\sqrt{r^{2}-\delta^{2}}}\right), \pi\ -\arctan\left(\frac{\delta}{\sqrt{r^{2}-\delta^{2}}}\right)\right]\right\}\,.\\
\end{align}
$$
Here, we define $0<\delta<r<\frac{1}{2}$ to maintain the shape of the contour. See here for how I came up with the sets above even though the link has a slightly different problem. Down below is a visual of what the union of the sets looks like.
$$
\text{Counterclockwise Dogbone/Dumbbell Contour }\mathcal{C}
$$
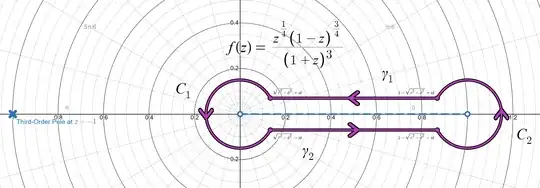
Here is an animation I made of how the counterclockwise traveling works.
We write the integral over $\mathcal{C}$ as
$$
\oint_{\mathcal{C}}f=\int_{\gamma_1}f+\int_{C_1}f+\int_{\gamma_2}f+\int_{C_2}f\,.
$$
Applying $\delta \to 0^+$ then $r \to 0^+$ in that specific order, we get
$$
\lim_{r \to 0^+}\lim_{\delta \to 0^+}\oint_{\mathcal{C}}f=\lim_{r \to 0^+}\lim_{\delta \to 0^+}\int_{\gamma_1}f+\lim_{r \to 0^+}\lim_{\delta \to 0^+}\int_{C_1}f+\lim_{r \to 0^+}\lim_{\delta \to 0^+}\int_{\gamma_2}f+\lim_{r \to 0^+}\lim_{\delta \to 0^+}\int_{C_2}f
$$
Evaluating the integral over $\gamma_1$ and taking the iterated limits, we get
$$
\begin{align}
\lim_{r \to 0^+}\lim_{\delta \to 0^+}\int_{\gamma_1}f &= \lim_{r \to 0^+}\lim_{\delta \to 0^+}\int_{\sqrt{r^{2}-\delta^{2}}-1}^{-\sqrt{r^{2}-\delta^{2}}}f(-t+i\delta)\left(-dt\right)\\
&\overset{-t=x}= -\lim_{r \to 0^+}\lim_{\delta \to 0^+}\int_{\sqrt{r^{2}-\delta^{2}}}^{1-\sqrt{r^{2}-\delta^{2}}}f(x+i\delta)\,dx \\
&= -\lim_{r \to 0^+}\lim_{\delta \to 0^+}\int_{\sqrt{r^{2}-\delta^{2}}}^{1-\sqrt{r^{2}-\delta^{2}}}\frac{\left|x+i\delta\right|^{\frac{1}{4}}\left|1-\left(x+i\delta\right)\right|^{\frac{3}{4}}\exp\left(\frac{i}{4}\arg\left(x+i\delta\right)\right)\exp\left(\frac{3i}{4}\arg\left(1-\left(x+i\delta\right)\right)\right)}{\left(1+x+i\delta\right)^{3}}\,dx\\
&= -\lim_{r \to 0^+}\int_{r}^{1-r}\frac{x^{\frac{1}{4}}\left(1-x\right)^{\frac{3}{4}}\exp\left(\frac{i}{4}\cdot0\right)\exp\left(\frac{3i}{4}\cdot2\pi\right)}{\left(1+x\right)^{3}}\,dx\\
&= i\mathcal{I}\,.
\end{align}
$$
I'll leave it up to you to prove that
$$
\lim_{r \to 0^+}\lim_{\delta \to 0^+}\int_{\gamma_2}f = \mathcal{I}\,.
$$
To evaluate the integral over $C_2$ with the iterated limits, we first bound the modulus of that integral as $\delta \to 0^+$. We have
$$
\begin{align}
\left|\lim_{\delta \to 0^+}\int_{C_{2}}f\right| &= \left|\lim_{\delta \to 0^+}\int_{-\pi+\arctan\left(\frac{\delta}{\sqrt{r^{2}-\delta^{2}}}\right)}^{\pi-\arctan\left(\frac{\delta}{\sqrt{r^{2}-\delta^{2}}}\right)}f(1+re^{it})\left(rie^{it}\,dt\right)\right| \\
&= \left|ri\lim_{\delta \to 0^+}\int_{-\pi+\arctan\left(\frac{\delta}{\sqrt{r^{2}-\delta^{2}}}\right)}^{\pi-\arctan\left(\frac{\delta}{\sqrt{r^{2}-\delta^{2}}}\right)}\frac{\left|1+re^{it}\right|^{\frac{1}{4}}\left|1-\left(1+re^{it}\right)\right|^{\frac{3}{4}}\exp\left(\frac{i}{4}\arg\left(1+re^{it}\right)\right)\exp\left(\frac{3i}{4}\arg\left(1-\left(1+re^{it}\right)\right)\right)}{\left(1+1+re^{it}\right)^{3}}e^{it}\,dt\right| \\
&=r^{\frac{7}{4}}\left|\lim_{\delta \to 0^+}\int_{-\pi+\arctan\left(\frac{\delta}{\sqrt{r^{2}-\delta^{2}}}\right)}^{\pi-\arctan\left(\frac{\delta}{\sqrt{r^{2}-\delta^{2}}}\right)}\frac{\left|1+re^{it}\right|^{\frac{1}{4}}\exp\left(\frac{i}{4}\arg\left(1+re^{it}\right)\right)\exp\left(\frac{3i}{4}\arg\left(-re^{it}\right)\right)}{\left(2+re^{it}\right)^{3}}\,dt\right|\\
&= r^{\frac{7}{4}}\left|\int_{-\pi}^{\pi}\frac{\left|1+re^{it}\right|^{\frac{1}{4}}\exp\left(\frac{i}{4}\arg\left(1+re^{it}\right)\right)\exp\left(\frac{3i}{4}\arg\left(-re^{it}\right)\right)}{\left(2+re^{it}\right)^{3}}\,dt\right| \\
&\leq r^{\frac{7}{4}}\int_{-\pi}^{\pi}\left|\frac{\left|1+re^{it}\right|^{\frac{1}{4}}\exp\left(\frac{i}{4}\arg\left(1+re^{it}\right)\right)\exp\left(\frac{3i}{4}\arg\left(-re^{it}\right)\right)}{\left(2+re^{it}\right)^{3}}\right|\,dt \\
&\leq r^{\frac{7}{4}}\int_{-\pi}^{\pi}\frac{\left(r^{2}\sin^{2}t+\left(1+r\cos t\right)^{2}\right)^{\frac{1}{8}}}{\left(2-r\right)^{3}}\,dt\,. \\
\end{align}
$$
With that upper bound in mind, we take $r \to 0^+$ and use the Squeeze Theorem to prove that
$$
\lim_{r\to0^+}\left|\lim_{\delta \to 0^+}\int_{C_{2}}f\right| = 0\,.
$$
This implies
$$
\lim_{r\to0^+}\lim_{\delta \to 0^+}\int_{C_{2}}f = 0\,.
$$
I'll leave it up to you to prove that
$$
\lim_{r\to0^+}\lim_{\delta \to 0^+}\int_{C_{1}}f = 0\,.
$$
Gathering these four results together, we go back to our dumbbell/dogbone contour integral and get
$$
\begin{align}
\require{cancel}
\lim_{r \to 0^+}\lim_{\delta \to 0^+}\oint_{\mathcal{C}}f&=i\mathcal{I}+\cancelto{0}{\lim_{r \to 0^+}\lim_{\delta \to 0^+}\int_{C_1}f}+\mathcal{I}+\cancelto{0}{\lim_{r \to 0^+}\lim_{\delta \to 0^+}\int_{C_2}f} \\
\frac{1}{1+i}\lim_{r \to 0^+}\lim_{\delta \to 0^+}\oint_{\mathcal{C}}f &= \mathcal{I}\,. \\
\end{align}
$$
Next, we use the Principle of Deformation of Contours to transform $\mathcal{C}$ into this keyhole-like contour comprised of the union of sets below:
$$
\begin{align}
\Gamma &:= \left\{Re^{it} \in \mathbb{C}: t\in\left[-\pi+\arctan\left(\frac{\delta}{\sqrt{R^{2}-\delta^{2}}}\right), \pi-\arctan\left(\frac{\delta}{\sqrt{R^{2}-\delta^{2}}}\right)\right]\right\} \\
\lambda_1 &:= \left\{t-1+i\delta: t\in\left[1-\sqrt{R^{2}-\delta^{2}},-\sqrt{r^{2}-\delta^{2}}\right]\right\} \\
\gamma_3 &:= \left\{-1-re^{-it}\in\mathbb{C}: t\in\left[\arctan\left(\frac{\delta}{\sqrt{r^{2}-\delta^{2}}}\right), 2\pi-\arctan\left(\frac{\delta}{\sqrt{r^{2}-\delta^{2}}}\right)\right]\right\} \\
\lambda_2 &:= \left\{-t-1-i\delta\in\mathbb{C}: t\in\left[\sqrt{r^{2}-\delta^{2}}, \sqrt{R^{2}-\delta^{2}}-1\right]\right\}\,. \\
\end{align}
$$
Just like the dumbbell/dogbone, we define $0<\delta<r<\frac{1}{2}$ to maintain the shape of the contour. We also let $R \gg 1$. See here for how I came up with the sets above even though the link has a slightly different problem. Down below is a visual of what the union of the sets looks like.
$$
\text{Counterclockwise Keyhole-Like Contour }\mathcal{C}
$$
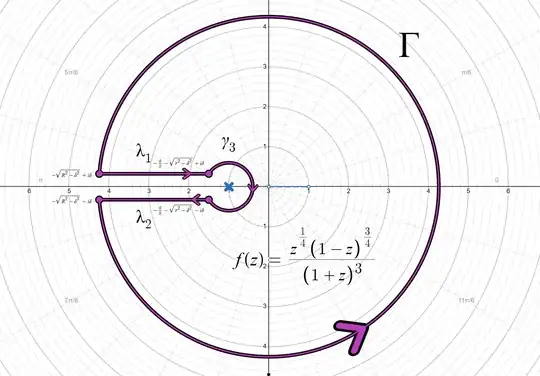
Click here for an animation for what the contour looks like being traversed in the positive direction.
We write the integral over $\mathcal{C}$ as
$$
\oint_{\mathcal{C}}f=\int_{\Gamma}f+\int_{\lambda_1}f+\int_{\gamma_3}f+\int_{\lambda_2}f\,.
$$
Applying $\delta\to-^+$ on both sides, we get
$$
\lim_{\delta\to0^+}\oint_{\mathcal{C}}f=\lim_{\delta\to0^+}\int_{\Gamma}f+\lim_{\delta\to0^+}\int_{\lambda_1}f+\lim_{\delta\to0^+}\int_{\gamma_3}f+\lim_{\delta\to0^+}\int_{\lambda_2}f\,.
$$
Evaluating the integral over $\lambda_1$ and taking the limit, we get
$$
\begin{align}
\lim_{\delta\to0^+}\int_{\lambda_1}f &= \int_{1-\sqrt{R^{2}-\delta^{2}}}^{-\sqrt{r^{2}-\delta^{2}}}\frac{\left|t-1+i\delta\right|^{\frac{1}{4}}\left|1-\left(t-1+i\delta\right)\right|^{\frac{3}{4}}\exp\left(\frac{i}{4}\arg\left(t-1+i\delta\right)\right)\exp\left(\frac{3i}{4}\arg\left(1-\left(t-1+i\delta\right)\right)\right)}{\left(1+t-1+i\delta\right)^{3}}dt \\
&= \int_{1-R}^{-r}\frac{\left|t-1\right|^{\frac{1}{4}}\left|2-t\right|^{\frac{3}{4}}}{t^{3}}\exp\left(\frac{i}{4}\cdot\pi\right)\exp\left(\frac{3i}{4}\cdot2\pi\right)dt \\
&\overset{t\mapsto -t}= -\exp\left(\frac{7\pi i}{4}\right)\int_{r}^{R-1}\frac{\left|t+1\right|^{\frac{1}{4}}\left|2+t\right|^{\frac{3}{4}}}{t^{3}}dt\,. \\
\end{align}
$$
I'll leave it up to you to prove that
$$
\lim_{\delta\to0^+}\int_{\lambda_2}f = \exp\left(-\frac{i\pi}{4}\right)\int_{r}^{R-1}\frac{\left|t+1\right|^{\frac{1}{4}}\left|2+t\right|^{\frac{3}{4}}}{t^{3}}dt\,.
$$
We now have
$$
\require{cancel}
\lim_{\delta\to0^+}\oint_{\mathcal{C}}f=\lim_{\delta\to0^+}\int_{\Gamma}f+\bcancel{\lim_{\delta\to0^+}\int_{\lambda_1}f}+\lim_{\delta\to0^+}\int_{\gamma_3}f+\bcancel{\lim_{\delta\to0^+}\int_{\lambda_2}f}\,.
$$
Applying $r\to0^+$ on both sides and knowing that $\int_{\Gamma}f$ does not depend on $r$, we get
$$
\lim_{r\to0^+}\lim_{\delta\to0^+}\oint_{\mathcal{C}}f=\lim_{\delta\to0^+}\int_{\Gamma}f+\lim_{r\to0^+}\lim_{\delta\to0^+}\int_{\gamma_3}f\,.
$$
Going back to the equality involving $\mathcal{I}$, we have
$$
\mathcal{I} = \frac{1}{1+i}\lim_{\delta\to0^+}\int_{\Gamma}f+\frac{1}{1+i}\lim_{r\to0^+}\lim_{\delta\to0^+}\int_{\gamma_3}f\,.
$$
Applying $R\to\infty$ on both sides and knowing that $\mathcal{I}$ and $\int_{\gamma_3}f$ do not depend on $R$, we get
$$
\mathcal{I} = \frac{1}{1+i}\lim_{R\to\infty}\lim_{\delta\to0^+}\int_{\Gamma}f+\frac{1}{1+i}\lim_{r\to0^+}\lim_{\delta\to0^+}\int_{\gamma_3}f\,.
$$
Next, we evaluate the first iterated limit by bounding its modulus as follows:
$$
\begin{align}
\left|\lim_{\delta\to0^+}\int_{\Gamma}f\right| &= \left|\lim_{\delta\to0^+}\int_{-\pi+\arctan\left(\frac{\delta}{\sqrt{R^{2}-\delta^{2}}}\right)}^{\pi-\arctan\left(\frac{\delta}{\sqrt{R^{2}-\delta^{2}}}\right)}f\left(Re^{it}\right)\left(Rie^{it}dt\right)\right|\\
&= \left|\int_{-\pi}^{\pi}\frac{\left|Re^{it}\right|^{\frac{1}{4}}\left|1-Re^{it}\right|^{\frac{3}{4}}\exp\left(\frac{i}{4}\arg\left(Re^{it}\right)\right)\exp\left(\frac{3i}{4}\arg\left(1-Re^{it}\right)\right)}{\left(1+Re^{it}\right)^{3}}Rie^{it}dt\right|\\
&\leq \int_{-\pi}^{\pi}\left|\frac{\left|Re^{it}\right|^{\frac{1}{4}}\left|1-Re^{it}\right|^{\frac{3}{4}}\exp\left(\frac{i}{4}\arg\left(Re^{it}\right)\right)\exp\left(\frac{3i}{4}\arg\left(1-Re^{it}\right)\right)}{\left(1+Re^{it}\right)^{3}}Rie^{it}\right|dt \\
&= \int_{-\pi}^{\pi}\left|\frac{R^{\frac{5}{4}}\left(R^{2}\sin^{2}t+\left(1-R\cos t\right)^{2}\right)^{\frac{3}{8}}}{\left(1+Re^{it}\right)^{3}}\right|dt \\
&\leq \int_{-\pi}^{\pi}\frac{R^{\frac{5}{4}}\left(R^{2}\sin^{2}t+\left(1-R\cos t\right)^{2}\right)^{\frac{3}{8}}}{\left(R-1\right)^{3}}dt \\
\end{align}
$$
Then we take $R \to \infty$ and use the Squeeze Theorem to prove that
$$
\lim_{R\to\infty}\left|\lim_{\delta\to0^+}\int_{\Gamma}f\right| = 0\,.
$$
This implies
$$
\lim_{R\to\infty}\lim_{\delta\to0^+}\int_{\Gamma}f = 0\,.
$$
As for the other integral, we have
$$
\begin{align}
\frac{1}{1+i}\lim_{r\to0^+}\lim_{\delta\to0^+}\int_{\gamma_3}f &= \frac{1}{1+i}\lim_{r\to0^+}\lim_{\delta\to0^+}\int_{\arctan\left(\frac{\delta}{\sqrt{r^{2}-\delta^{2}}}\right)}^{2\pi-\arctan\left(\frac{\delta}{\sqrt{r^{2}-\delta^{2}}}\right)}f\left(-1-re^{-it}\right)d\left(-1-re^{-it}\right) \\
&= \frac{1}{1+i}\lim_{r\to0^+}\int_{0}^{2\pi}f\left(-1-re^{-it}\right)d\left(-1-re^{-it}\right) \\
&=\frac{1}{1+i}\oint_{\gamma_4}f(z)\,dz\,,
\end{align}
$$
where $\gamma_4$ is a small circle of radius $r$ centered at $z=-1$ traveling clockwise.
By Cauchy's Residue Theorem, we get
$$
\frac{1}{1+i}\oint_{\gamma_4}f(z)\,dz = -\frac{2\pi i}{1+i}\mathop{\mathrm{Res}}_{z=-1}f(z)
$$
Just scroll to the top of this answer to see what the answer to the residue calculation is.
Now we have
$$
\require{cancel}
\mathcal{I} = \frac{1}{1+i}\cancelto{0}{\lim_{R\to\infty}\lim_{\delta\to0^+}\int_{\Gamma}f}+3\pi\cdot2^{-\frac{23}{4}}\,.
$$
We finally conclude with
$$
\bbox[13px,#fffbe9,border:5px inset #670000]{\int_{0}^{1}\frac{x^{\frac{1}{4}}\left(1-x\right)^{\frac{3}{4}}}{\left(1+x\right)^{3}}dx = 3\pi\cdot2^{-\frac{23}{4}}}
$$
and we're finished!