The geometry behind $\cos 48^{\circ}$ as decomposition of $\sin 18^{\circ}$

Question

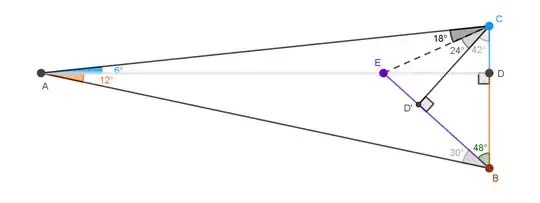
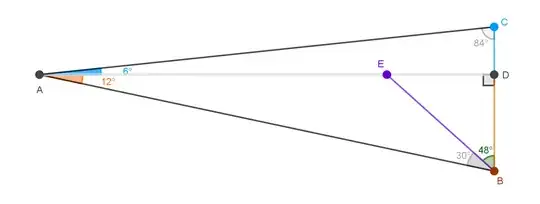
Consider a $\triangle ABC$ with $\angle A = 18^{\circ},~\angle B = 78^{\circ},~\angle C = 84^{\circ}$. The height $\overline{AD} \perp \overline{BC}$ splits the apex into $\angle DAC = 6^{\circ}$ and $\angle DAB = 12^{\circ}$ as shown below, sideways.

Prove for a point $E \in \overline{AD}$ along the height, $|BE| = |BC|$ if and only if $\angle EBC = 48^{\circ}$. Purely geometric proofs are preferred (using Law of Sines is fine), but the intrigue of this problem is more conveniently expressed trigonometrically: $$\cos 48^{\circ} = \frac{ \tan 12^{\circ} }{ \tan 6^{\circ} + \tan 12^{\circ} } = \frac{ \sin 12^{\circ} \cos 6^{\circ} }{ \cos 12^{\circ} \sin 6^{\circ} + \sin 12^{\circ} \cos 6^{\circ} } $$ or $$\cos 48^{\circ} = \frac{ \sin 12^{\circ} \cos 6^{\circ} }{ \sin 18^{\circ} } \hspace{154pt}$$ Namely, $\cos 48^{\circ}$ as a fraction somehow exactly expresses the addition-formula-decomposition of $\sin 18^{\circ}$ into $6^{\circ} + 12^{\circ}$.

I have proved the above algebraically, along with several other interesting trigonometric identities associated with this construct. The special angle here is $48^{\circ}$, but in the end the identities become "pentagonal" (it's all about angles $18^{\circ}$ and $36^{\circ}$).

The trigs deserve a separate post (and I've noticed many existing posts about related identities). Here I'm looking for a geometric argument or insight. Here are some vaguely relevant examples demonstrating how I imagine trigonometry-heavy questions can be "understood": a, b (simpler examples for "pentagonal identity"), and 1, 2, 3, 4, 5 (more complex constructs). One can see that I'm pretty lost now and these reference might not even make sense for my context.

Maybe Ceva's Theorem is necessary ($E$ being the concurrent point inside $\triangle ABC$), but I don't know how to implement it in this context without ending up doing trigonometry. The concept of Ceva is certainly geometric (and not algebraic), and embedding in a 30-gon (or 15-gon) is good perspective, but I just don't want crucial steps to rely on trigonometric calculations. In case this whole thing is not as simple as I thought, techniques from projective geometry is welcomed.

This problem emerged from an equilateral triangle configuration involving $\{6^{\circ}, 12^{\circ}, 18^{\circ} \}$. The original context is unhelpful and distracting; as an auxiliary equilateral triangle, it seems like a massive overkill (accompanying angles $\{66^{\circ}, 54^{\circ}, 42^{\circ}, 24^{\circ}\}$ etc are seen left and right). I isolated the construct to present it here.

Failed Attempts

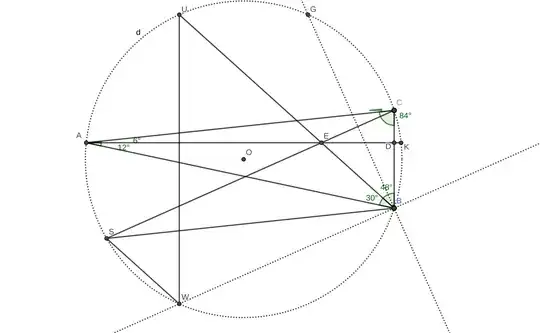
My hunch is that the most sensible underlying geometry of this $48^{\circ}$ (relating to splitting $18^{\circ}$ into $6^{\circ} + 12^{\circ}$) is to view $\overline{BE}$ as one of the isosceles edges of $\triangle BEB'$ as shown below. Point $B'$ in the top right corner of the diagram is the reflection of $B$ with respect to $\overline{AD}$. 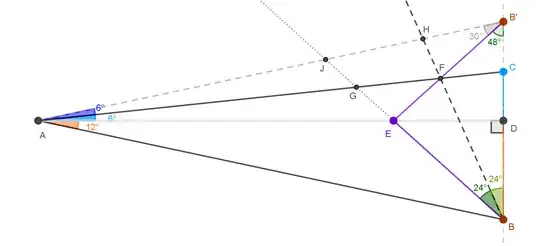The intended perspective is to view the auxiliary bigger isosceles $\triangle ABB'$ as the "whole picture", to take advantage of the symmetries (with respect to $\overline{AD}$ and $\overline{BH}$) that wasn't explicit.

Everywhere you look, there are angles of special values, angle-biesctors, similar triangles, and isosceles triangles. For example, trying to prove the congruency $\triangle BEB' \equiv \triangle BCG$ seems like a viable strategy. However, so far I haven't found a way out of the tautology of angle-chasing and length-matching.

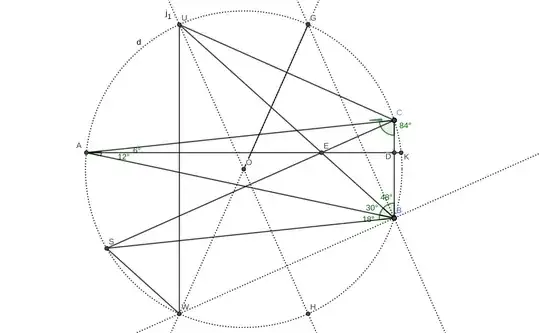
A similar idea about hidden symmetry is to reflect the entire $\triangle ABC$ with respect to $\overline{BH}$ such that $\overline{BE}$ is the base for the mirrored apex $A'$. The other mirrored vertices are $B'=B$ and $C'=E$ as seen below. This also seemed promising due to the existing $\angle E$ matching $\angle C = 84^{\circ}$ (as in its half $\angle BED = 42^{\circ}$), but it led nowhere.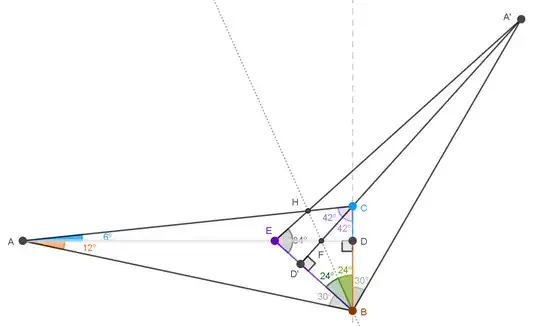

Alternatively, going small, to gain insight from the auxiliary $\overline{CF} \perp \overline{BE}$ constructed below, I failed in the same fashion, just seeing things work nicely but making circular arguments and getting redundant results.

Answer 1

In the picture BG is perpendicular on EC. External bisector of angle $ABC$ is perpendicular at BG, so $EC||BW$where W is where external bisector intersects the circumcircle d of triangle ABC.Extention oCE from E meets d at S so we have:

$\overset{\large\frown}{BC}=\overset{\large\frown}{SW}$

If triangle BCE is isosceles then we must have:

$\angle BEC=\angle BCE\Rightarrow \frac{\overset{\large\frown}{BC}+\overset{\large\frown}{US}}2=\frac{\overset{\large\frown}{SW}+\overset{\large\frown}{BW}}2$

Which results in:

$\overset{\large\frown}{US}=\overset{\large\frown}{BW}$

Now in circle d we have:

$\overset{\large\frown}{CU}+\overset{\large\frown}{US}+2\overset{\large\frown}{BC}+\overset{\large\frown}{WB}=360^o$

$\overset{\large\frown}{BC}=2(12+6)=36$

$\Rightarrow 2\overset{\large\frown}{US}+\overset{\large\frown}{CU}=360-2\times 36=288^o $

Suppose arcs CU, US and WB must have integer values,$288$ is divisible by $3$, so if $WB=US=CU$ then we have:

$\overset{\large\frown}{CU}=\frac{288}3=96^o$

Which gives :

$\angle CBE=\frac{96}2=48^o$

Note: I could not show that $UW||BC$ which deduces the equality of arcs CU and BW.

Update:

In the picture, in triangle UBC the bisector of angle UBC meets the perpendicular bisector of base UC at G . GW is the diameter of d because $\angle GBW=90^o$. UH is another diameter of d. We have:

$\overset{\large\frown}{UG}=\overset{\large\frown}{WH}$

H is the mid point of arc WB, so we have:

$\overset{\large\frown}{UG}=\overset{\large\frown}{GC}=\overset{\large\frown}{WH}=\overset{\large\frown}{HC}$

SO:

$\overset{\large\frown}{UC}=\overset{\large\frown}{WB}$