5

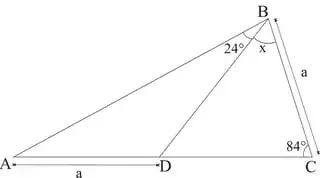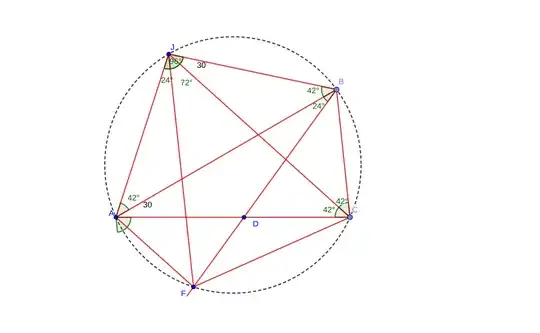
enter image description here

I have tried to solve this problem for hours but i still can't figure it out.

Does anyone know what problem name is this or have an approach to this problem? Thanks. I want a proof without trigonometry, just more elementary geometry

Find $x$ if $AD=CB$. Justify geometrically. can i have a proof like the highest score answer shown in the link above? if can please help

Meurtino
  • 59
  • 1
    Welcome to MSE. It is in your best interest that you type your posts (using MathJax) instead of posting links to pictures. – José Carlos Santos Jan 06 '25 at 10:52
  • Welcome to Math.SE! ... Please edit your question to include what you've tried. This will help people target their responses to best serve you, without wasting time explaining things you already understand or using techniques beyond your current skill level. Moreover, knowing what hasn't worked will help people avoid attempting the same approaches; or, someone may be able to nudge you to a complete solution without starting from scratch and potentially duplicating your effort. ... Good luck! – Blue Jan 06 '25 at 11:00
  • sine rule gives $$a \Big (\frac{1 + \frac{ \sin x}{\sin 84}}{\sin(x+24)}\Big) = \frac{a}{\sin ( x + 24 + 84)}$$ Solve for x in this equation – Anon Jan 06 '25 at 11:06
  • $\angle{BAD}=72-x$ and $\angle{BDC}=96-x$ so you have $$\sin(72-x)\sin(96-x)=\sin(24)\sin(84)$$. – Ataulfo Jan 06 '25 at 12:31
  • 1
    Here is a similar problem: https://math.stackexchange.com/q/4295312/947379 – ACB Jan 06 '25 at 13:32
  • 1
    Please show your work (even if its a trigo proof), else this post might be closed by the community, despite the interest in it. – Calvin Lin Jan 06 '25 at 15:30

1 Answers1

4

enter image description here

In picture J is midpoint of $arc AB=2\times 84=168^o$, so we have:

$\angle AJB=96^o$

$\angle AJF=24^o\Rightarrow \angle FJB=72^o$

Triangle AJB is isosceles so:

$\angle JBA=42^o$

$\angle JFB=42^o\Rightarrow BC||JF \Rightarrow arc JB=arc FC\Rightarrow \angle FJC=\angle JCB=42^o$

$\Rightarrow \angle CJB=72-42=30^o\Rightarrow \angle BAC=30^o$

Which finally gives:

$\angle CBD=42^o$

We may also use the $BC=AD$

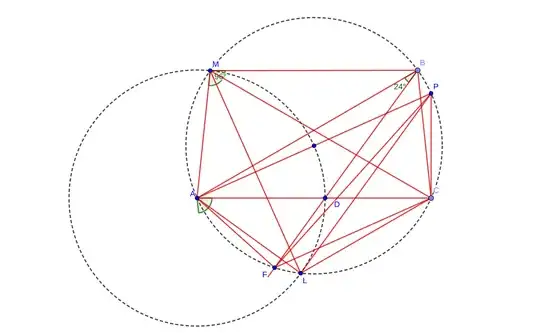
enter image description here

As shown in picture we connect M to L , so the perpendicular bisector of LM is the diameter of circumcircle , it meets the circle at P , so:

$\angle ACP=90^o\Rightarrow \angle BCP=90-84=6^o\Rightarrow arc BP=12^o $

So the auxiliary circle center on A and radius R passes through the center of the circumcircle and so their radii are equal. This means:

$PL||BF\Rightarrow arc FL=arc BP=12^o$

$arc AF=49^o\Rightarrow arc AL=49+12=60^o$

This implies that $AD=BC=AL=R$ the radius of the circumcircle , so $arc BC=60^o\Rightarrow \angle BAC=30^o$

Finally:

$\angle ABC= 180-(30+84)=66^o\Rightarrow x=CBD=66-24=42^o$

sirous
  • 12,694
  • 1
    Why does $\angle JFB=42^o\Rightarrow BC||JF$ ? – Dan Jan 07 '25 at 12:31
  • ►Where is $\overline{AD}=\overline{BC}$ data used?

    ►►Knowing by trigonometry that angle $x=42$ it is "natural" to note that $84=2\times42$ and the rest comes. I wanted to say that it is very improbable to solve geometrically if $x$ is not an integer (in degrees)and I find another answer (however I was hesitant because of my answer don't use $\overline{AD}=\overline{BC}$ neither.

     – Ataulfo Jan 07 '25 at 12:46
  • @Dan, You are right . I included the use of BC=AD in the answer. – sirous Jan 07 '25 at 16:15
  • I reiterate Dan's question, which (to me) is a huge hole in your proof. It's not clear to me what you're doing. If you're using $BC = AD$ to imply that $BC \parallel JF$, then that should be made much clearer. $\quad$ I suspect you were trying to work from both ends, but then didn't keep track of which implications you had. – Calvin Lin Jan 07 '25 at 22:42
  • Also, please provide clear definitions of your terms. EG What is your new figure? Are the 2 circles of equal diameter? Furthermore, why must $AO = AD$? Is this an assumption that you're making? – Calvin Lin Jan 07 '25 at 22:45
  • Why does $arc BP = 12^\circ \Rightarrow \angle APL = 30^\circ$? $BP$ and $AL$ do not seem to be that related. – Calvin Lin Jan 07 '25 at 22:50
  • @CalvinLin, I edited my answer and corrected some errors. Certainly we must give reason for every point we use in our solutions. For example why $FC||AP$. I used the accurate construction, but could not prove it. I have seen many tricks like this in solutions of other users, i.e they used a thing that must be proved as a fact. As a whole I see this site a place for cooperation of users to solve problems rather than a place for competition. – sirous Jan 08 '25 at 06:49
  • "I used the accurate construction, but could not prove it." This needs to be stated. IE You have a proof by accurate construction, and not a "theoretical" proof. That would help the rest of us understand how your statement should be interpreted. $\quad$ FWIW It is my opinion that accurate construction is not a valid a proof method (because like you mentioned "they used a thing that must be proved as a fact" implying that it wasn't proved), though I understand that others might consider it is valid. I agree it is helpful to guide how to think about the question. – Calvin Lin Jan 08 '25 at 17:17