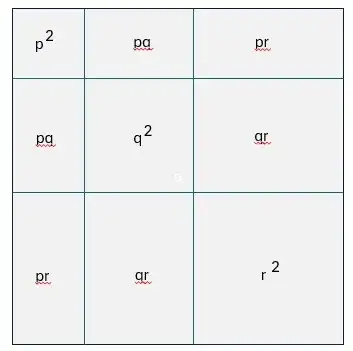
Identity
$$(p+q+r)^2=p^2+q^2+r^2+2qr+2pr+2pq\tag{1}$$
has a classical visual representation (Fig. 1) which constitutes a "graphical proof" for positive $p,q,r$ :
$\textit{Fig. 1 : Classical visualization of identity (1)}.$
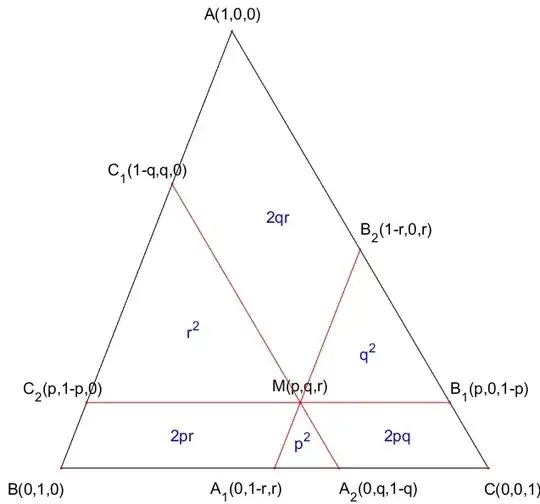
I have found a different graphical representation of (1) using barycentric coordinates as given on Fig. 2 :
$$\textit{Fig. 2 : Another visualization of identity (1) in terms of barycentric coordinates.}$$
where $(p,q,r)$ (normalized with $p+q+r=1$) are the barycentric coordinates wrt "base triangle" $ABC$ of the common point to all triangles and parallelograms.
Indeed, the different terms of the RHS of (1) are interpretable as relative areas of triangles or parallelograms ("relative" meaning in this context "divided by the area of triangle $ABC$").
The proofs are straightforward : for example, the relative area of the small triangle on the left, (with one of its sides on $AB$), is equal to the determinant :
$$\left|\matrix{(1-q)&p&p\\q&(1-p)&q\\0&0&r}\right|=r((1-p)(1-q)-pq)=r(1-p-q)=r^2$$
where the barycentric coordinates of the vertices are placed in columns.
Same type of computations for the other areas.
My question is :
I would like to present this nice elementary result to a certain audience. I am 100% sure that this result has already been found (and maybe applied to interesting problems), but haven't been able to find any anterior reference. Could somebody find one ?
Remarks :
- There is more to say about Fig. 2 : it provides a visualization of the barycentric coordinates of $M$ as the following ratios of lengths :
$$p=\frac{A_1A_2}{BC},\ \ q=\frac{B_1B_2}{AC},\ \ r=\frac{C_1C_2}{AB}$$
(easy proof).
- A same type of result exists with 3D barycentric coordinates (sometimes called tetraedric coordinates) $(p,q,r,s)$ with respect to a tetrahedron $ABCD$, this time with relative volumes in correspondence with identity :
$$(p+q+r+s)^3=p^3+q^3+...+3q^2r+3q^2s+...$$