0

$P$ is a point inside the triangle $ABC.$Lines are drawn through $P$,parallel to the sides of the triangle.The three resulting triangles with the vertex at $P$ have areas $4,9$ and $49$ sq.units.The area of the triangle $ABC$ is
$(A)75\hspace{1cm}(B)120\hspace{1cm}(C)195\hspace{1cm}(D)144$
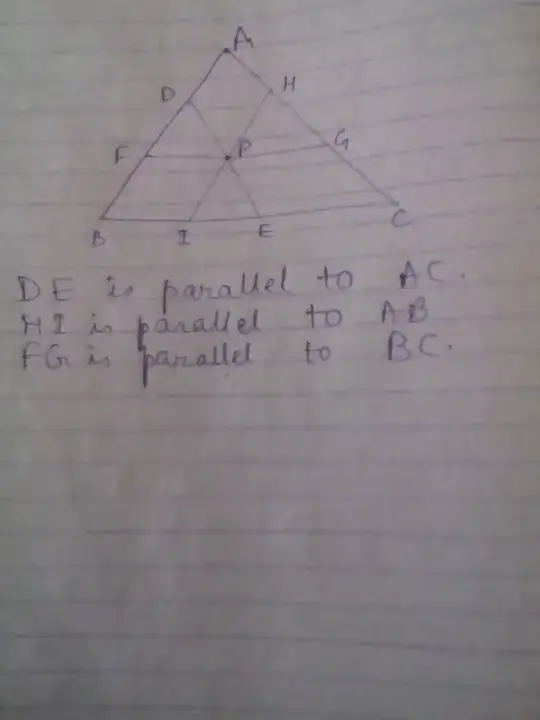
enter image description here

I could not solve this problem.Please help me.

user1442
  • 1,366

1 Answers1

2

We may suppose that $[\triangle{PIE}]=49,[\triangle{DPF}]=4,[\triangle{HGP}]=9$.

$\triangle{HGP}$ and $\triangle{PEI}$ are similar and $HP:PI=\sqrt{9}:\sqrt{49}=3:7$.

So, since $IP:IH=7:10$, $$[\triangle{IPE}]:[\triangle{IHC}]=7^2:10^2.$$ Hence, $[\triangle{IHC}]=100$, so $[\text{parallelogram $PGCE$}]=100-9-49=42$.

Similarly, we can get $[\text{parallelogram $PFBI$}]$ and $[\text{parallelogram $ADPH$}]$ :

$$[\text{parallelogram $PFBI$}]=(\sqrt 4+\sqrt{49})^2-4-49=28$$ $$[\text{parallelogram $ADPH$}]=(\sqrt 4+\sqrt 9)^2-4-9=12.$$

Hence, the answer is

$$12+4+28+49+42+9=144.$$

mathlove
  • 151,597