Find the value of the segment parallel to the side of the triangle by an interior point

Question

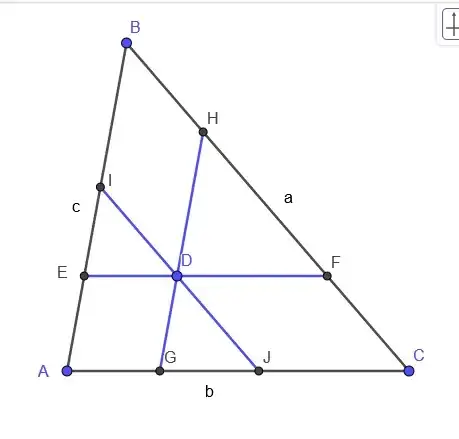
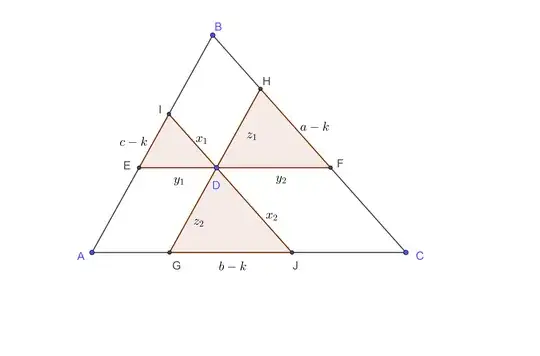
Let P be a point inside a triangle of sides a, b, and c through which they are drawn parallel to the sides of the triangle. If the parallel segments between the sides of the triangle have the same measure, find their value. (Answer:$\dfrac{2}{\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}}$)

I tried but I didn't find the solution

$\triangle ABC \sim \triangle AJI\\ \frac{JI}{a} =\frac{AJ}{b}=\frac{AI}{c}\\ \triangle ABC \sim \triangle BEF\\ \frac{EF}{b}=\frac{BF}{a}=\frac{BE}{c}\\ \triangle ABC \sim \triangle CGH\\ \frac{GH}{c}=\frac{CH}{a}=\frac{CG}{b}\\ GH=IJ=EF$

Answer 1

We have $$[AIJ]+[EBF]+[GHC]-[DHF]-[GDJ]-[EID]=[ABC].\tag1 $$ Dividing the equation by $[ABC]$ one obtains: $$ \frac{[AIJ]}{[ABC]}+\frac{[EBF]}{[ABC]}+\frac{[GHC]}{[ABC]}-\frac{[DHF]}{[ABC]}-\frac{[GDJ]}{[ABC]}-\frac{[EID]}{[ABC]}=1\tag2 $$ or $$ \left(\frac xa\right)^2+\left(\frac xb\right)^2+\left(\frac xc\right)^2- \left(1-\frac xa\right)^2-\left(1-\frac xb\right)^2-\left(1-\frac xc\right)^2=1,\tag3 $$ where $[XYZ]$ means the area of the triangle $XYZ$ and $x$ is the measure of the segments.

Resolving $(3)$ with respect to $x$ one obtains after simple algebra: $$ x=\frac2{\frac1a+\frac1b+\frac1c}.\tag4 $$

Explanation:

$(1):$ The union of the triangles $AIJ$, $EBF$ and $GHC$ gives the triangle $ABC$. However the union is not disjoint. For example the intersection of the triangles $AIJ$ and $EBF$ is the triangle $EID$. Therefore the areas of the triangles $DHF$, $GDJ$ and $EID$ will be included twice in the area sum of the triangles $AIJ$, $EBF$ and $GHC$. Thus to obtain the area of the triangle $ABC$ this doubly counted area should be subtracted.

$(2)$: Division by $[ABC]$.

$(3)$: All triangles $AIJ$, $EBF$, $GHC$, $DHF$, $GDJ$, $EID$ and $ABC$ are similar with similarity coefficients $$ (AIJ):(DHF):(ABC)=\frac xa:1-\frac xa:1 $$ and similarly for the other triangles. The areas of similar triangles relate as squares of similarity coefficients.

$(4)$: The square terms cancel, so that there remains a linear equation to solve.

Answer 2

Refer to the figure, let $k$ be the common measure

i.e. $EF=GH=IJ=x_1+x_2=y_1+y_2=z_1+z_2=k$.

Note that $\Delta EID \sim \Delta GDJ \sim \Delta DHF \sim \Delta ABC $

From $\Delta EID \sim \Delta ABC $, we have

$$\frac{x_1}{a}=\frac{y_1}{b}=\frac{c-k}{c}=1-\frac{k}{c} \tag{1}$$

Similarly $\Delta GDJ \sim \Delta ABC \implies $

$$\frac{x_2}{a}=\frac{z_2}{c}=\frac{b-k}{b}=1-\frac{k}{b} \tag{2}$$

$\Delta DHF \sim \Delta ABC \implies $

$$\frac{y_2}{b}=\frac{z_1}{c}=\frac{a-k}{a}=1-\frac{k}{a} \tag{3}$$

$(1)+(2)+(3) \implies$

$$\frac{x_1}{a} + \frac{y_1}{b} + \frac{x_2}{a} + \frac{z_2}{c} + \frac{y_2}{b}+\frac{z_1}{c}=2 \times \left( 1-\frac{k}{c} + 1-\frac{k}{b}+1-\frac{k}{a} \right)$$

$$\frac{x_1+x_2}{a}+\frac{y_1+y_2}{b}+\frac{z_1+z_2}{c}=6 -2 \times \left( \frac{k}{a}+\frac{k}{b}+\frac{k}{c}\right)$$

$$\frac{k}{a}+\frac{k}{b}+\frac{k}{c}=6 -2 \times \left( \frac{k}{a}+\frac{k}{b}+\frac{k}{c}\right)$$

$$3k \times \left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right)=6 $$

$$k=\frac{2}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}$$