Find $x$ if $AD=CB$. Justify geometrically.

Question

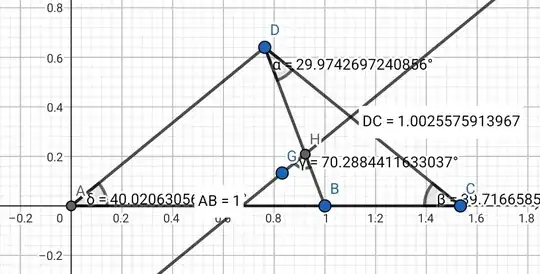
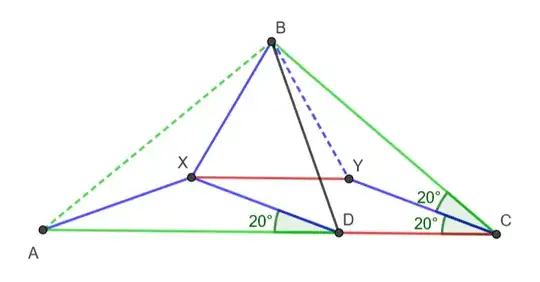
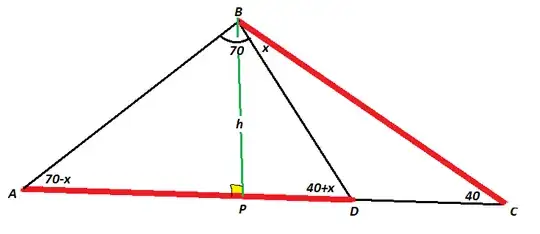
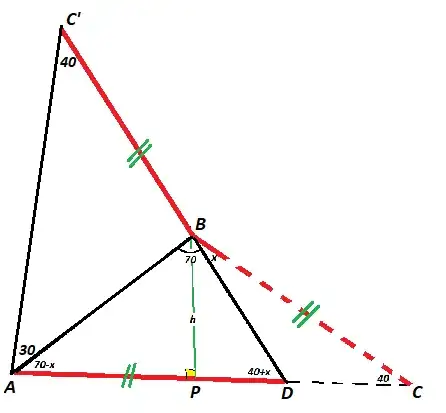
I need help with this geometry question. Find $x$ if $AD=CB$. Justify geometrically.

I tried plotting it on GeoGebra and found that $x=30\unicode{176}$ but I don't know how to prove it, I also tried with a system of linear equations but it has no solution:

$\begin{cases}70\unicode{176}+x_2+x_3=180\unicode{176}\\[5pt] 70\unicode{176}+x_1+40\unicode{176}+x_2=180\unicode{176}\\[5pt] 40\unicode{176}+x_1+\left(180\unicode{176}-x_3\right)=180\unicode{176}\end{cases}$

I also tried drawing the heights of the $2$ triangles to get right triangles but I end up with more unknowns.
Thanks in advance.

Answer 1

Pick $D'$ on $AC$ such that $CD'=CB$. Then triangle $CBD'$ is isosceles with a top angle of $40^\circ$. The remaining two angles are $70^\circ$.

Now take a look at points $D,D'$. By hypothesis $AD=CD'$ so $D,D'$ are symmetric with respect to the midpoint of $AC$.

Moreover, $BD, BD'$ are also symmetric with respect to the bisector of the angle $\angle ABC$ since $\angle ABD = \angle D'BC = 70^\circ$.

This is only possible if the triangle $ABC$ is isosceles and $AB=BC$. This gives $\angle B = 100^\circ$ and $\angle DBC = 30^\circ$.

---

To conclude that the triangle is isosceles do the following

• consider a triangle $AD'B'$, translating the triangle $DCB$ until $AD'$ and $DC$ overlap.

• then $\angle ABD'= \angle AB'D'$, showing that $A,D',B,B'$ are on the same circle

• by construction $BB'||AC$, thus $A,D',B,B'$ are the vertices of an isosceles trapeze. The non-parallel edges and diagonals are equal, implying that the triangle $ABC$ is isosceles also.

Answer 2

Let $X$ be the circumcenter of $ABD$. Since $\angle ABD = 70^\circ$, we have $\angle XDA = 90^\circ - \angle ABD = 20^\circ$.

Let $Y$ be so that $XDCY$ is a parallelogram. Note that $ACYX$ is an isosceles trapezoid because $AC\parallel XY$ and $AX=DX=CY$. Also note that $\angle YCD =\angle XDA = 20^\circ$, hence $$\angle BCY = \angle BCD - \angle YCD = 40^\circ - 20^\circ = 20^\circ.$$ We are given $BC=AD$. Hence by SAS the triangles $XDA$, $YCB$ are congruent. In particular $YB=XA=XB$.

Since $ACYX$ is an isosceles trapezoid, the segments $AC$, $YX$ have the same perpendicular bisector, call it $\ell$. Since $BX=BY$, the point $B$ lies on $\ell$. Hence the whole figure is symmetric. In particular $\angle CAB = \angle BCA = 40^\circ$, hence $\angle ABC = 100^\circ$ and $\angle DBC = 30^\circ$.

Answer 3

If you're familiar with sine rule, then apply it to $BDC$ and $BDA$ to get

$$\frac{BC}{\sin 40^\circ + x } = \frac{BD}{\sin 40^\circ}, \frac{AD}{\sin 70^\circ} = \frac{BD}{\sin 70^\circ - x}.$$

Since $BC = AD$, hence

$$ \frac{\sin 40^\circ + x } {\sin 40^\circ} = \frac{BC}{BD} = \frac{AD}{BD} = \frac {\sin 70^\circ} {\sin 70^\circ - x}.$$

Thus (with a bit of work), $x = 0^\circ, 30^\circ$.

Note: It is arguable if $ x = 0^\circ$ is a valid solution, as one may argue that the diagram indicates $ 0^\circ < x < 110^\circ $. However, it bears to bote that for $x = 0^\circ$, we do have $BC = AD$.

Answer 4

$$ AD=BC=1;$$

Mark angles by angle chasing ( angle sum 180 and external angle sum equals sum of two internal angles )

$$AP+PD= h \cot (70 -x)+h \cot (40 + x)=1,~h / BC= 1. \sin (40) $$

Solving numerically we directly get

$$ x=30, h\approx 0.643788;$$

This can be also put down by inspection or by careful trial & error.

EDIT1;

Next, the numerical solution $DBC'=x=180$ deg (continuation of BD) also supplies a second solution. The second possible construction satisfying same geometry is sketched below superimposed with the first one.

It is noted in conclusion that

$$ BA = BC= BC'=AD.$$