Are these circles the same size? (Sangaku problem with a semicircle and two pairs of circles in an equilateral triangle)

Question

The diagram shows an equilateral triangle, a black semicircle, two congruent red circles and two congruent green circles. Wherever things look tangent, they are tangent.

Let $g=\text{radius of green circles}$, $r=\text{radius of red circles}$

Without using a computer, determine whether $g$ and $r$ are equal.

Without using a computer, I proved that $g\ge r$.

I tried to prove that $g>r$, but have not found a way.

(Using a computer, I found that $\frac{g}{r}=\frac{2\sqrt3+2\sqrt6-1-4\sqrt{189\sqrt2-154\sqrt3+108\sqrt6-264}}{33\sqrt2-26\sqrt3+19\sqrt6-45}\approx 1.0001686$.)

Answer 1

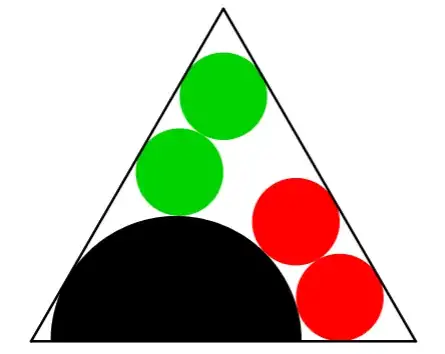
tl;dr: If the green and red circles are the same size, then a rotated copy of the semicircle is tangent to a red circles. The tangencies lead to inconsistent Pythagorean conditions in the (purple) right triangles shown in the figure.

---

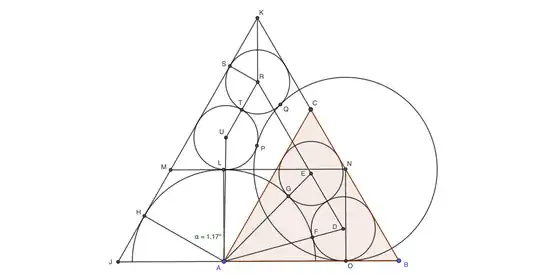
Consider equilateral $\triangle ABC$ with (black) semicircle centered at $O$ on $AB$, and (red) circles centered at $P$ and $Q$. Let the semicircle be tangent to $AC$ at $U$, let $\bigcirc P$ be tangent to $BC$ and $AB$ at $R$ and $T$, and let $\bigcirc Q$ be tangent to $BC$ at $S$.

Also, rotate the semicircle $120^\circ$ about the triangle's center to have center $O'$ on $AC$ and tangent point $U'$ on $BC$. If OP's green circles are congruent to the reds, then this rotated semicircle should be tangent to $\bigcirc Q$. We'll see if that's viable.

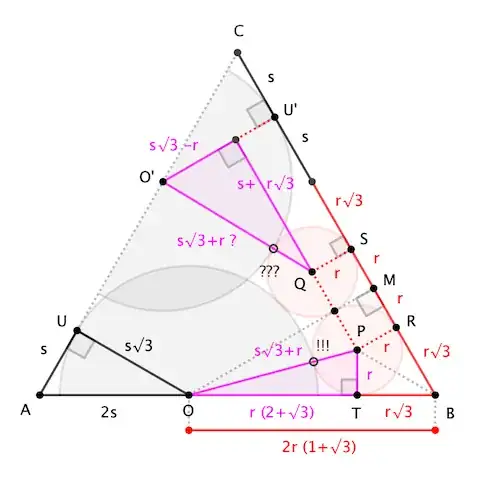
Now, if semicircle $O$ is tangent to the circles, then $O$ lies on the perpendicular bisector of $PQ$; thus, the perpendicular from $O$ meets $BC$ meets midpoint $M$ of $RS$, so that $\bigcirc P$ is the incircle of $\triangle OBM$.

Exploiting $30^\circ$-$60^\circ$-$90^\circ$ triangles ... If the radius of the semicircle is $s\sqrt{3}$, we have $|AU|=|CU'|=s$ and $|AO|=2s$; if the common radius of the circles is $r$, then $|RM|=|SM|=r$, $|BR|=|BT|=r\sqrt{3}$, and $|BO|=2|BM|=2r(1+\sqrt{3})$.

Observe that the semicircle-circle tangency is encoded in right triangle $\triangle OPT$, giving the Pythagorean condition $$(s\sqrt{3}+r)^2 = r^2 + r^2(2+\sqrt{3})^2 \tag{1}$$ We could explicitly solve this for, say, $s$ in terms of $r$, but we needn't bother. All we need to notice is $s\sqrt{3}$ is definitely not an integer multiple of $r$.

We conclude that the triangle $QO'$ is the hypotenuse of a right triangle with legs $s+r\sqrt{3}$ and $s\sqrt{3}-r$. Hence, if semicircle $O'$ is tangent to $\bigcirc Q$, then $|QO'|=s\sqrt{3}+r$, and $$\begin{align} (s\sqrt{3}+r)^2 = (s+r\sqrt{3})^2+(s\sqrt{3}-r)^2 &\quad\to \quad (s-r\sqrt{3})^2=0 \\ &\quad\to\quad |OU| = s\sqrt{3}=3r \tag{2} \end{align}$$ However, a semicircle-to-circle radius ratio of $3:1$ violates the observation about $(1)$. Consequently, OP's red and green circles are not the same size. $\square$

---

Addendum. Here's a sketch of a slightly more straightforward approach to relation $(2)$.

Let $C'$ complete equilateral $\triangle OBC'$. The tangency of semicircle $O$ with the red circles implies that the distance from $OC'$ to $AC$ is the semicircle's radius; hence, the rotated semicircle $O'$ is automatically tangent to this line.

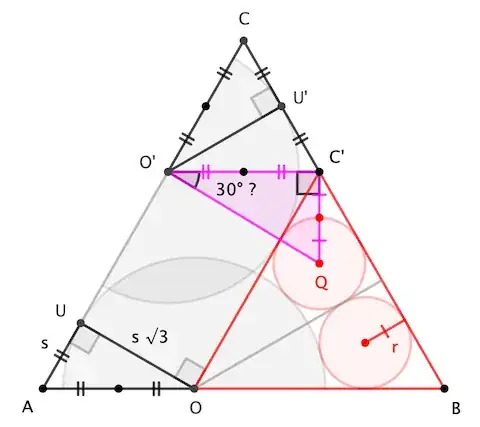
For semicircle $O'$ to be tangent to red circle $\bigcirc Q$, they'd have to share a point of tangency with $OC'$; thus, $O'Q\perp OC'$, which implies that $\triangle O'QC'$ is $30^\circ$-$60^\circ$-$90^\circ$, giving immediately $s=r\sqrt{3}$ (reconfirming $(2)$).

Answer 2

Let's name $R$ the radius of the large circle, while $r$ and $g$ are the radii of the small circles, as explained in the question. Moreover, we can take the side of the triangle as $1$. Then we have (see figure below): $$ AO+ON+NB=AB, $$ that is: $$ \tag1 {2\over\sqrt3}R+\sqrt{(R+r)^2-r^2}+\sqrt3 r=1; $$ and $$ OQ+QP={\sqrt3\over2}(AB-AO) $$ that is: $$ \tag2 \sqrt{(R+r)^2-r^2}+r={\sqrt3\over2}-R. $$ We can eliminate the square root between $(1)$ and $(2)$ to obtain: $$ \tag3 r={\sqrt3-1\over4\sqrt3}(\sqrt3-2R). $$ Plugging that into $(2)$ we can solve for $R$: $$ \tag4 R=\frac{15}{2}+5 \sqrt{3}-6 \sqrt{2} -3\sqrt{6}. $$ To find $g$, note that: $$ AE+AD+DJ+JC=AC, $$ that is: $$ {R\over\sqrt3}+\sqrt{4Rg}+2g+\sqrt3g=1 $$ whence: $$ \tag5 g=2-\sqrt3+{15\sqrt3-26\over\sqrt3}R- {2\over\sqrt3} \sqrt{(78-45\sqrt3)R+(336-194\sqrt3)R^2}. $$ We could plug $(4)$ into $(3)$ and $(5)$, to find exact expressions for $g$ and $r$. But to prove $r\ne g$ we can follow another route, namely equate expressions $(3)$ and $(5)$ and solve for $R$. After eliminating the square root, we are left with a quadratic equation, whose discriminant vanishes. The solution is then quite simple: $$ R={6\sqrt3-3\over22}. $$ But this is different from result $(4)$, hence $r\ne g$, as it was to be proved.

Answer 3

The construction giving rise to the question seems to be as follows: Given equilateral triangle $ABC$ with inscribed circles centered on $D$, $E$, join $AD$, $AE$ and draw semicircle with center $A$ and radius $AF=AG$. Extend $BA$, make $\angle HAJ=30^o$, and complete equilateral triangle $BJK$.

Thus we know the conditions of the problem are possible: two equal circles externally tangent to a semicircle and to each other, and all internally tangent to an equilateral triangle on which the semicircle is based.

As OP observes https://puzzling.stackexchange.com/questions/129842/can-the-circles-fit-inside-the-triangle, tangent $MLN\parallel JB$ makes$$\triangle MNK\cong \triangle ABC$$so that circles centered on $U$, $R$ are equal to each other and to the circles centered on $D$, $E$. But since tangent point $L$ does not lie on $AU$, circle $U$ is tangent to $MN$ but not to the semicircle ($\angle UAL\approx1.2^o$), and hence as @Blue and @Intelligenti pauca show, equal green circles tangent to $\triangle BJK$ and to the semicircle will not equal the equal red circles.

Answer 4

I don't think the green and red circles have the same size: when you stretch the black semicircle until it reaches the right bottom point of the triangle, then the red circles can't exist, but it's still possible to create the green circles, meaning that the red and the green circles' radiuses are not always equal.

Hereby an image of what I'm talking about: (plenty of room to draw the green circles, but the red ones can't exist)

A bit clearer (with the red circles coinciding in point $B$):