"The Tiger's Paw" (Sangaku problem with six circles in an equilateral triangle, show that the ratio of radii is three to one.)

Question

In the diagram below, the triangle is equilateral; the four black circles are congruent; wherever things look tangent, they are tangent.

Show that the ratio of the green to red radii is three to one.

I have found a solution, which I will post below, but it is quite complicated. I am looking for a more elegant solution.

---

Why I find this interesting

As I show in my self-answer, the ratio of the green to black radii is a messy number: it is $(1-s):s$ where

$$16s^6-\left(24+8\sqrt{3}\right)s^4+4\sqrt{3}s^3+\left(13+6\sqrt{3}\right)s^2-\left(4+3\sqrt{3}\right)s+\frac34=0.$$

But somehow the ratio of the green to red radii is simply three to one.

And this result means that another red circle fits perfectly in the space below the green circle (and of course another red circle fits in the upper right corner).

Context

This is the latest of my geometrical puzzles; previous ones are here and here.

Answer 1

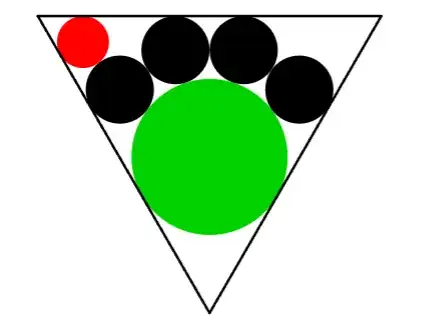
The strategy

Assuming that the green radius is $3$, we will draw a circle with radius $1$ tangent to the top and right sides of the triangle, then show that this circle must be tangent to the rightmost black circle.

Definitions & assumptions

• Assume that the green radius is $3$, and that the equation of the green circle is $x^2+y^2=3^2$.
• $b=$ radius of the black circles
• $2\theta=$ angle subtended at the centre of the green circle by a black circle
• $s=\sin\theta$
• $P$ is the point where the green circle touches the right side of the triangle.
• $Q$ is the point where the rightmost black circle touches the right side of the triangle.

Establishing some equations satisfied by $s=\sin\theta$

We have:

• $s=\frac{b}{b+3}\implies b=\frac{3s}{1-s}$.
• The coordinates of $P$ and $Q$ are $\left(\frac{3\sqrt3}{2},-\frac32\right)$ and $\left((b+3)\sin 3\theta+\frac{\sqrt3}{2}b,(b+3)\cos 3\theta-\frac12b\right)$, respectively. Letting the gradient of $PQ$ equal $\sqrt3$, gives $(b+3)\cos 3\theta-\frac12b+\frac32=\sqrt3\left((b+3)\sin 3\theta+\frac{\sqrt3}{2}b-\frac{3\sqrt3}{2}\right)$.

Solving the two equations together, using $\sin 3\theta\equiv 3s-4s^3$ and $\cos 3\theta\equiv \sqrt{1-s^2}\left(1-4s^2\right)$, we get

$$\sqrt{1-s^2}=\frac{2-(4+3\sqrt3)s+4\sqrt3s^3}{4s^2-1}\tag 1$$

Squaring both sides gives

$$f(s)=0\tag 2$$

where

$$f(x):=16x^6-\left(24+8\sqrt{3}\right)x^4+4\sqrt{3}x^3+\left(13+6\sqrt{3}\right)x^2-\left(4+3\sqrt{3}\right)x+\frac34$$

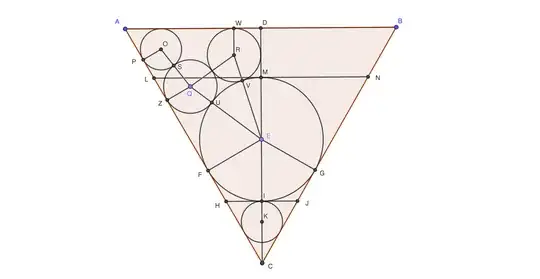
New circle $C$

Draw circle $C$ with radius $1$ tangent to the top and right sides of the triangle.

Let $d=$ distance between the centre of $C$ and the centre of the rightmost black circle.

We want to show that $d=b+1$, which would imply that $C$ is tangent to the rightmost black circle.

We have

$$d^2=\left(\frac{1}{\sqrt3}((b+3)\cos\theta+b+3)-(b+3)\sin 3\theta\right)^2+\left((b+3)\cos\theta+b-1-(b+3)\cos 3\theta\right)^2$$

Basic algebra, utilising equation $(1)$, shows that

$$d^2-(b+1)^2=g(s)\tag 3$$

where

$$g(x):=\frac{6\left(64\sqrt3x^6-(64+64\sqrt3)x^4+(40+8\sqrt3)x^3+(8+12\sqrt3)x^2-(2+6\sqrt3)x+1\right)}{(4x^2-1)(1-x)^2}$$

Defining a key function $h(x)$

With some help from Wolfram, we define

$$h(x):=(4x^2-1)(x-1)^2(8x^3+(4+4\sqrt3)x^2-(4+2\sqrt3)x-6-3\sqrt3)$$

We can show that $h(s)\ne 0$ by the following argument. Clearly $0<s<\frac12$ (because if the diagram had two black circles instead of four, then $s$ would equal $\frac12$). So the quadratic factors of $h(s)$ do not equal $0$. And it is easy to show that the cubic factor of $h(s)$ does not equal $0$, by finding the turning points on $h(x)$ and calculating $h\left(\frac12\right)$.

Then using polynomial expansion, we can verify that

$$g(x)h(x)\equiv 24f(x)(8\sqrt3x^3+(12+4\sqrt3)x^2-2x-\sqrt3-2)$$

From equation $(2)$ we have $f(s)=0$, so $g(s)=0$.

Then from equation $(3)$, we have $d=b+1$.

Conclusion

$\therefore C$ is tangent to the rightmost black circle.

$\therefore C$ is congruent with the red circle.

$\therefore$ The red circle has radius $1$.

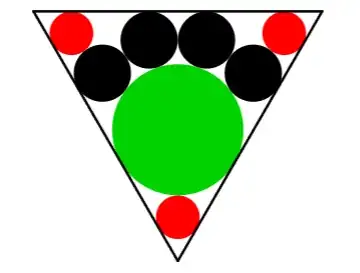
$\therefore$ The ratio of the green to red radii is three to one.

Answer 2

Here's a pass at a solution.

Cutting the paw in half and toppling it gives the figure below.

The chain of tangent circles $\bigcirc A$, $\bigcirc B$, $\bigcirc C$ —of radii $a$, $b$, $c$— are tangent to the "horizontal" at $A'$, $B'$, $C'$. We readily deduce $$|A'B'| = 2\sqrt{ab} \qquad |B'C'|=2\sqrt{bc} \tag1$$ Further, $\bigcirc A$ is tangent to $OP$, which is inclined at a $60^\circ$ angle to the horizontal, so that $$|OA'|=a\sqrt{3} \tag2$$ Point $P$ is such that $OP\perp PC$, and $\bigcirc D$ (of radius $B$) is tangent to $\bigcirc B$, $\bigcirc C$, $OP$, and $PC$. The viability of the figure is encoded in Pythagorean relations in the right triangles $\triangle BDP$ and $\triangle CDR$ (with hypotenuses $2b$ and $b+c$), whose legs are parallel and perpendicular to $OP$. To get at those relations, we exploit $30^\circ$-$60^\circ$-$90^\circ$ triangles throughout (also with legs parallel and perpendicular to $OP$), to find $$\begin{align} |BQ| &= |OB'|\cdot\frac{\sqrt{3}}{2} -|BB'|\cdot\frac{1}{2}-b \\ &=\frac12 \left(3 (a - b) + 2\sqrt{3ab}\right) \tag3\\ |DQ| &= |B'C'|\cdot\frac12-|BB'|\cdot\frac{\sqrt{3}}{2}+|CC'|\cdot\frac{\sqrt{3}}{2}-b \\ &= \frac12 \left( (c-b)\sqrt{3} -2b+ 2 \sqrt{b c} \right) \tag4 \\ \\ |DR| &= b \tag5 \\ |CR| &= |OC'|\cdot\frac{\sqrt3}{2} - |CC'|\cdot\frac12 - b \\ &= \frac12 \left(3 a - 2 b -c + 2 \sqrt{3ab} + 2 \sqrt{3bc} \right) \tag6 \end{align}$$ Defining $b_2:=\sqrt{b}$, $c_2:=\sqrt{c}$, $d_2:=\sqrt{3a}$ (the last because $\sqrt{3}$ is attached to $\sqrt{a}$ throughout the calculations), the two Pythagorean relations are ugly quartics in $b_2$: $$\begin{align} 0 &= 4 \sqrt3 b_2^4 - 4 b_2^3 (3 d_2 + (2 + \sqrt3) c_2) - 2 b_2^2 (d_2^2 + (1 + 2\sqrt3) c_2^2) \\ &\quad + 4 b_2 (d_2^3 + \sqrt3 c_2^3) + d_2^4 + 3 c_2^4 \tag7 \\[6pt] 0 &= 4 b_2^4 - 8 b_2^3 (d_2 + \sqrt3 c_2) + 8 b_2^2 c_2 (\sqrt3 d_2 + c_2) \\ &\quad + 4 b_2 (d_2 + \sqrt3 c_2) (d_2^2 - c_2^2) + (d_2^2 + c_2^2) (d_2^2 - 3 c_2^2) \tag8 \end{align}$$ Failing to find a clever way to eliminate $b_2$, I resorted to hitting the equations with Mathematica's Resultant function to obtain $$ (c_2-d_2)^3 (3 c_2 - d_2) (c_2 + d_2)\left(\cdots\right) = 0\tag9$$ where $(\cdots)$ decomposes into two linear and three cubic factors in $c_2$ whose positive real roots correspond to extraneous values $0.0529\ldots$, $0.0893\ldots$, $0.5773\ldots$ for $\sqrt{c/a}$ (which clearly should be greater than $1$). For the visible factors in $(9)$, only $c_2-d_2$, corresponding to solution $c=3a$, is viable. This confirms OP's claim. $\square$

Answer 3

OP starts with the four equal and tangent black circles and asks why the radius of the green is triple that of the red. The following approach is from a different direction: first identifying the family of circles with radii in the $\frac{3}{1}$ ratio (green/red), and then, supposing a red circle in the upper left angle of the equilateral triangle, seeking, with help from GeoGebra,the conditions under which the equilateral triangle can admit four equal and tangent black circles.

I. In equilateral triangle $ABC$ with altitude $AD$ let $E$ be the center of a circle tangent to $CA$, $CB$ at $F$, $G$. Draw tangents $LMN$ and $HIJ$. Since the incircle center of an equilateral triangle divides the altitude in a $\frac{2}{1}$ ratio, then in equilateral triangles $CLN$, $CHJ$ altitude $CM=3CI$ and hence radius$$EM=3KI$$ II. Now construct a circle with radius $OP=KI$ tangent to $AC$, $AB$. This is a red circle.

What position of $E$ on altitude $CD$ can accommodate two equal circles $QU$, $RV$ tangent to each other, to circle $E$, and to side $AC$, circle $O$, side $AB$, and altitude $CD$?

Evidently we must have $EQ=ER$, $\angle REQ=2\angle DER$, and $RV=RW=QZ=QS$, where $RW$, $QZ$ are perpendiculars to $AB$,$AC$, respectively, with $S$ lying on circle $O$ on line $QO$.

This seems to require $\angle DER\approx 17.7^o$, $\angle REQ=2\angle DER\approx 35.4^o$, as in the GeoGebra figure above.

Some confirmation: Instead of angles $35.4^o/17.7^o$ in the two-to-one ratio, the two figures below have angles $36^o/18^o$ and $34^o/17^o$ In the left figure, circle $O$ has the required tangencies, but equal circle $N$ exceeds the triangle. In the right figure, again circle $Q$ is tangent but circle $P$ fails to touch side $DF$.

Thus it seems, of all possible circles centered on the altitude of an equilateral triangle and tangent to two of its sides, and thus having a radius triple that of the tangent circle beneath and of an equal circle placed in an upper corner, only one such green circle allows for the "fearful symmetry" of the Tiger's Paw.