Conjecture: For $n$ circles in a triangle, the maximum number of tangent points is $3n$.

Question

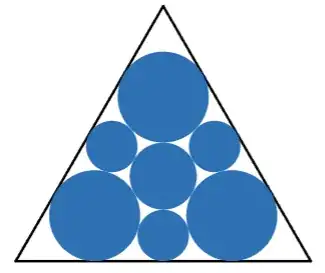
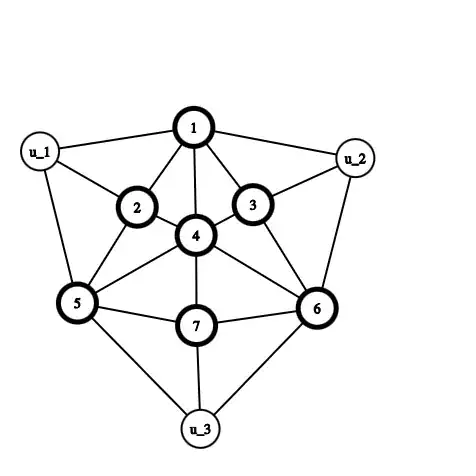
Is the following conjecture true: For $n$ non-overlapping circles (or disks) in a triangle, the maximum number of tangent points is $3n$.

The tangent points include points where two circles are tangent, and points where a circle is tangent to a side of the triangle.

For example, here are $7$ circles and $21$ tangent points.

My thoughts

The conjecture is not true for other polygons: for example, a single circle inscribed in a square has four tangent points.

Could this be related to the fact that a circle can be surrounded by at most six other circles of the same size?

I am not very familiar with graph theory, but I suspect that may be used here.

Context

I was playing with circles in triangles, and I started to wonder about he maximum number of tangent points.

Answer 1

I'm not entirely sure but I think the following works: Given a triangle and $n$ circles as above. Let us define a graph $G$ as follows.

Take $n+3$ vertices, identifying each circle with a vertex plus three additional vertices $u_1,u_2,u_3$ corresponding to the three sides of the triangle.

Now we add an edge between any two vertices, when the corresponding circles share a tangent point. Also add edges between $u_i$ and vertices corresponding to circles that are tangent to the corresponding triangle side.

One can check that $G$ defined in this way is planar. A famous result of planar graph theory is that a planar graph on $m\ge 3$ vertices can have at most $3m-6$ edges.

Therefore $G$ has at most $3(n+3)-6 -3 = 3n$ edges (because the edges $u_1u_2, u_1u_3, u_2u_3$ could be added to $G$ and it would remain planar). The edges in our graph correspond exactly to the tangent points. So we have $3n$ at most.

EDIT:

Here's a picture of how $G$ would look like for the $7$ circles and the triangle as in the question. The nodes $1-7$ correspond to the circles in the picture.

Answer 2

@Immanuel's answer answered the question perfectly. Here, I will slightly generalize that answer and show that the upper bound can be attained.

---

Consider $n$ non-overlapping circles inside a $k$-gon. As in @Immanuel's answer, we consider a vertex for each of the $n$ circles and each edge of the $k$-gon, so there are $n+k$ vertices. We add an edge between two vertices if the corresponding objects touch. This again yields a planar graph $G$, so the total number of edges is at most $3(n+k)-6$.

In fact, we can add $2k-3$ more edges to $G$ and still get another planar graph $G’$. These edges are added between the $k$ vertices associated with the edges of the $k$-gon: $k$ of these form a $k$-gon, and the remaining $k-3$ form diagonals on the outside. Therefore, the bound $3(n+k)-6$ applies to $G’$. This then gives the bound $$ 3(n+k)-6-(2k-3) = 3n+k-3, $$ on the maximum number of edges of $G$.

---

In fact, this bound can be achieved very easily. Start with a regular $k$-gon with a circle inscribed in it. This satisfies the bound for $n=1$. Pick a vertex of the $k$-gon, and consider the two edges that are incident to it. Add a new circle that touches the previous circle and these two edges. This adds $3$ tangent points for each new circle.